Glaubt man den täglichen Nachrichten, dann bedroht
eine globale Erwärmung die Menschheit.
Dafür sei das Treibhausgas CO2 hauptverantwortlich.
Klimaskeptiker bezweifeln, dass der Temperatur-Anstieg menschengemacht ist.
Was passiert,
wenn wir auf der Erde in den nächsten Jahrhunderten
fossilen Kohlenstoff nutzen wie bisher ?
In Zahlen:
Ich untersuche das dann im Jahr 2300 mögliche Scenario von 1600 ppm statt heutiger 400 ppm :
Zur Erwärmung der Erdatmosphäre durch CO2
von Rainer Schottlaender, Diplomphysiker
dT/dH = – g/Cp beschreibt den Temperaturverlauf in einer Planetenatmosphäre
Um zu verstehen wie CO2 die Temperatur beeinflusst beginnen wir bei Null:
Bild 1 zeigt die hypothetische 0 ppm CO2 Linie – – – – – über Guam

Bild 3 zeigt bei 1,3,5 und sieben Luftmassen Gegenstrahlung und Absorption:
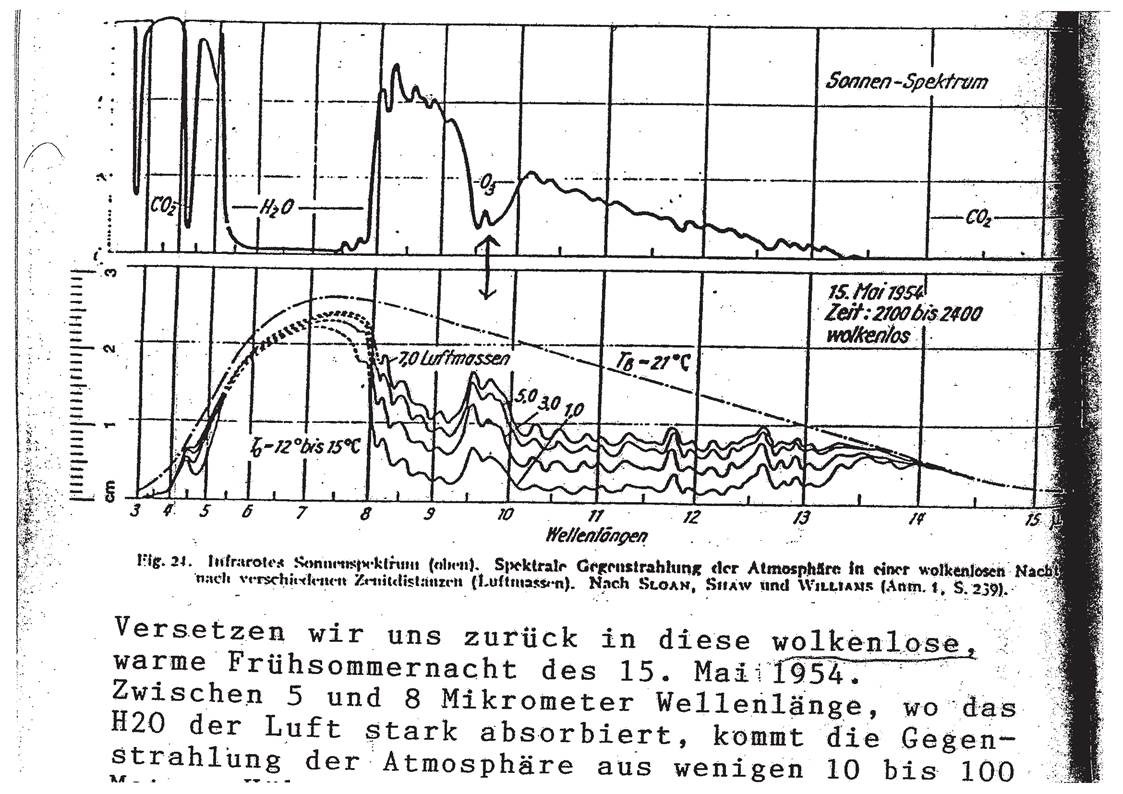
Ich betrachte und vermesse Fig.24:
1600 ppm CO2-Luft verschiebt die Absorption dieser 4,3 µm Bande in Fig.24
maximal um 2 mm x 4 mm = 8 mm2 bei einer Gesamtfläche von 15 x 120 = 1800 mm2
Dadurch zu erwartendes dT = dU/U x T/4 = 8/1800 x 300 K/4 = aufgerundet 0,4 K
Die Messung erfolgte mittags. Nachts liegt der Wert darunter.
Berechnung des Beitrages der 15 µm Bande zur globalen Erwärmung:
Hierzu Bild 2: Infrarotspektrum der Erde gemessen vom Satelliten Nimbus

Bei 667 cm^-1 misst der Satellit Strahlung mit 230 K-Intensität
= 90 Grad Temperaturdifferenz zu 320 K der Erdoberfläche.
Zwischen 630 und 700 cm^-1 … 110 Grad Temperaturdifferenz.
Durchschnittliche Temperatur und molare Masse der Luft in Abhängigkeit von der Höhe.."
Die Erhöhung von pCO2 von heutigen 400 ppm
auf von mir angenommene 1600 ppm im Jahr 2300
führt zu
– einer Verschiebung des 667 cm^-1 peaks
– einem Ausbeulen der Flanken zwischen 700 und 750 cm^-1 und 580 bis 620 cm^-1
Spektroskopie und Umweltphysik der Atmosphäre …
https://www.physi.uni-heidelberg.de › ~eisele › schuelerlabor › Spektrosko…
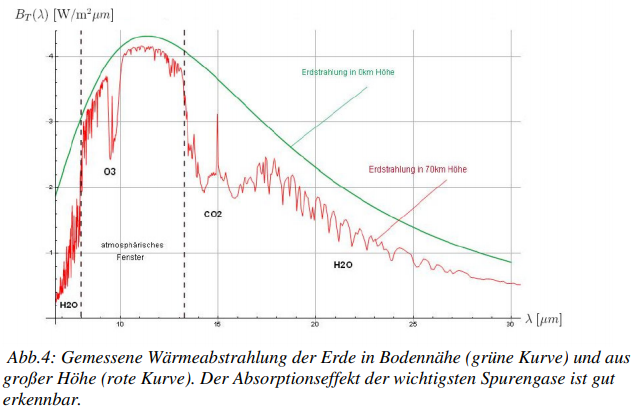
Ich verfolge die rote Kurve in dieser Grafik von 13 um bis 18 um.
Mit zunehmender Absorption kommt IR aus immer grösseren Höhen.
220-K-Strahlung , auch oben in Bild 2 sichtbar,
kommt aus der kältesten Schicht der Tropopause / Standard-Atmosphäre
Man sieht in Abb.4 bei 9,6 um …. die Wirkung von nur 3 mm Ozon
Bereits wenige ppm O3 sättigen diese Absorptionsbande.
Ich rechne mit global warming
durch das AuSbeulen der Flanken 12,5 .. 13 µm und 16 … 18 µm.
und mit global cooling
durch AuFbeulen bei 14 … 16 µm. (Größere Abstrahlhöhe/Temperatur)
Ich vermesse Abb.4 mit Zoom 175 % :
(0,2 W/m^2um) x 1 um = 0,2 W/m^2
Gesamtintegral ca. 2 W/m^2um x 50 um = 100 W/m^2
dU/U x T/4 = dT = 0,2/100 x 300/4 = 1,5 K
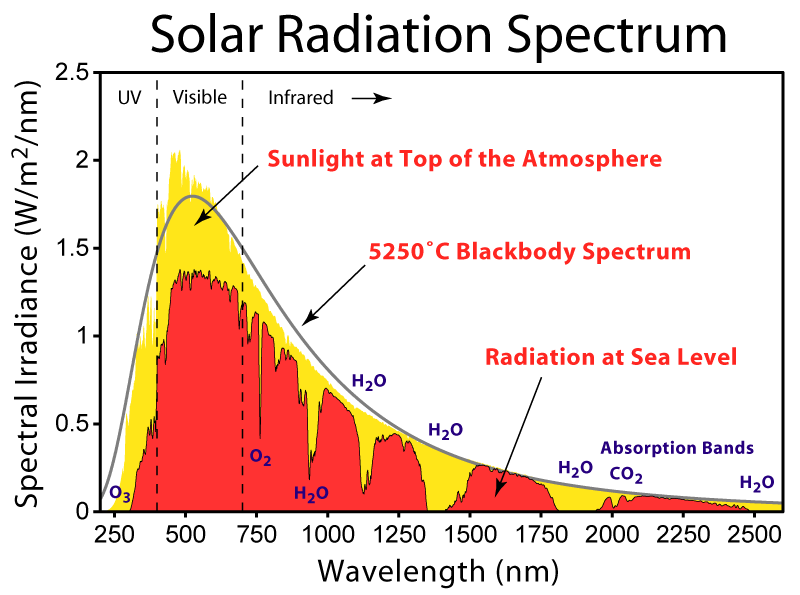
Spektrum der Sonne außerhalb der Atmosphäre und am Erdboden
im Vergleich zum Spektrum eines schwarzen Strahlers mit einer Temperatur von 5250°C …"
Viermal soviel CO2 in der Luft wie heute
verursacht mehr Absorption des direkten Sonnenlichtes bei 2000 … 2100 nm
und damit ein global cooling von ca.
( ( 0,1 W/m^2um x 50 nm = 5 W/m^2 ) / 1370 W/m^2 ) x 300 K/4 = 0,3 K
Saldo: +0,4 K + 1,5 K – 0,3 K = 1,6 K
Über Tag/Nacht und Bewölkung gemittelt liegt der Wert darunter.
Mein Ergebnis ist um den Faktor zehn beruhigender als die Lehrmeinung.
Ich erinnere an die vergleichbare Situation beim Spinat:
Es war ein Kommafehler.
——————————————————————————————–
Profil der Venusatmosphäre:
g = 8,87 m/s2
pCO2 = 90 bar.

Druck- und Temperaturverlauf
Diese Grafik zeigt: dT/dH = 500 K/50 km = 10 K/km
Cp CO2 = 0,85 J/gK ( Luft 1 J/gK)
g/Cp = 8,87 m/s^2 / 0,85 J/gK = ……….. 10 K/km
Die Formel dT/dH = – g/Cp erklärt denTemperaturverlauf einer Planetenatmosphäre.
Dieser wird bestimmt von der spezifischen Wärme Cp der Gashülle
und der Schwerkraft.
Nicht von den Strahlungseigenschaften der 90 bar/96 % CO2-Venus-Lufthülle.
Das gilt vergleichbar für Planet Erde
mit dT/dH = 5 … 8 K/km und 1 bar/99% O2/N2-Atmosphäre.
Zur zukunftsentscheidenden T(CO2)-Frage hier die vom IPCC lautstark angeführteLehrmeinung:


Der Strahlungsantrieb (RF für radiative forcing, auch Δ F {\displaystyle \Delta F} ) kann über eine lineare Beziehung mit der Änderung der globalen Gleichgewichtstemperatur an der Erdoberfläche ( Δ T S {\displaystyle \Delta T_{S}} ) verknüpft werden:[2]Δ T S = λ Δ F {\displaystyle \Delta T_{S}=\lambda \Delta F}

Mit λ = Parameter der Klimasensitivität mit der Einheit K/(W/m2).
Der durch die die Zunahme der CO2-Konzentrationen verursachte Strahlungsantrieb lässt sich wie folgt näherungsweise berechnen:[1][3]Δ F = 5 , 35 W m 2 ⋅ ln C C 0 {\displaystyle \Delta F=5,35{\mathrm {W} \over \mathrm {m} ^{2}}\cdot \ln {C \over C_{0}}}


Mit C = CO2-Konzentration der zu betrachtenden Atmosphäre in ppm, C0= Ausgangskonzentration der Vergleichsatmosphäre in ppm, Δ F {\displaystyle \Delta F} = resultierender Strahlungsantrieb in W/m²…"
Auf Venus angewendet :
DeltaF
= 5,35 W/m^2 x ln (90 bar pCO2/0,0004 bar pCO2) = 12,3
= 65 Watt/m^2
Tatsächlich wärmestrahlt 737-K-Venusboden 5,67 x 7,37^4
= 16728 Watt/m^2
https://de.wikipedia.org/wiki/Venus_(Planet)#Atmosph%C3%A4re :
Der starke Treibhauseffekt (man spricht hier auch vom Venus-Syndrom) ist hauptsächlich durch die Masse an Kohlendioxid bedingt, aber auch die geringen Spuren von Wasserdampf und Schwefeldioxid haben daran einen wesentlichen Anteil.
Er sorgt am Boden für eine mittlere Temperatur von 464 °C (737 K).[1]
Das liegt sehr weit über der ohne Treibhauseffekt berechneten Gleichgewichtstemperatur von −41 °C (232 K),…"
Ich korrigiere "wesentlich" mit diesem Gedankenexperiment:
Mein 1 m^2 Schreibtisch
stehe in dieser Minute auf der Venusoberfläche.
Über mir 50.000 Meter dicke Luft:

Zusammensetzung der Venus-Atmosphäre
Wikipedia = IPCC lehrt:
" .. In Bodennähe wurden bislang nur geringe Windgeschwindigkeiten von 0,5 bis 2 m/s gemessen. Durch die hohe Gasdichte entspricht das auf der Erde immerhin der Windstärke 4, das heißt, es kommt einer mäßigen Brise gleich, die Staub bewegen kann. Von dem auf die Venus einfallenden Sonnenlicht erreichen nur zwei Prozent die Oberfläche und ergeben eine Beleuchtungsstärke von etwa 5000 Lux.
Die Sichtweite dort beträgt wie an einem trüben Nachmittag rund drei Kilometer…"
Wie weit kommt die Infrarotstrahlung ? ….
… Dass die Atmosphäre der Venus von außen völlig undurchsichtig ist, liegt nicht an der großen Masse und Dichte der Gashülle, sondern hauptsächlich an einer stets geschlossenen Wolkendecke. Diese befindet sich mit ihrer Unterseite in einer Höhe von etwa 50 km und ist rund 20 km dick. Ihr Hauptbestandteil sind zu etwa 75 Masseprozent Tröpfchen aus Schwefelsäure"
… Nicht durch diese Wolken.
———————————————————————-
Ungeklärt :
Wohin führt die C-14 Spur ?:
14C in der Atmosphäre.[1]
https://de.wikipedia.org/wiki/Kernwaffen-Effekt :
" Seit dem Verbot der oberirdischen Kernwaffentests nimmt das 14C/12C-Verhältnis
in der Atmosphäre wieder ab …
In der Erdatmosphäre befinden sich 3000 Gigatonnen CO2,[2]
die im Mittel alle 3–5 Jahre vollständig ausgetauscht werden,[3]
wodurch die durch die Kernwaffenversuche eingebrachte Menge …. "
C-14-O2 Moleküle markieren chemisch fast identische
normale atmosphärische C-12-O2-Moleküle und begleiten deren Lebensweg .
Was geschah und geschieht
mit den bisher von der Menschheit emittierten
500 GtC x 44/12 = 1833 Gigatonnen CO2-Molekülen ? Irrt das nobelpreisgekrönte IPCC auch in dieser Frage ?

Hierzu ein Experiment:
Schotti´s Klimaglobus
Von schotti am 16. Februar 2011 Quelle: https://www.schottie.de/?p=650
Unsere Erde im Massstab 1 zu 2,6 mal 10 hoch 21 by volume
500 Gramm Wasser simulieren den Ozean
1,5 Liter Luft in dieser 2 Liter Glasflasche die 4 mal 10 hoch 18 qbm Atmosphäre
unter Normalbedingungen 1013 mbar.
Ich injiziere mit einer Spritze CO2 und messe wie schnell sich wieviel löst. Das Gerät plus CO2-Messkopf plus eine Reparatur/Eichung kostete mich 1000 DM.

Copyright 1990 – 2. Dezember 2019 : www.schottie.de
1
https://www.schottie.de/?p=11809
Gesendet: Mittwoch, 11. Dezember 2019 um 17:00 Uhr, "Allgemein ARD Morgenmagazin" , ard-morgenmagazin@daserste.de, info@br.de, info@daserste.de, "Erik Marquardt" , mail@bundestag.de, gerhard@sabathil.eu
Von: "Rainer Schottlaender"
An: "pressedienst@DasErste.de"
Betreff: sofort an Herrn Volker Herres , Programmdirektor ARD
Sehr geehrter Herr Herres,
sehr geehrte ARD-Redakteure mit naturwissenschaftlichem Studium:
Ihre SENDUNG MIT DER MAUS dürfen Sie gerne weitersenden.
Ursula von der Leyen`s Kindertraum von einem GREEN DEAL bitte nicht mehr:
https://www.tagesschau.de/ausland/green-deal-eu-kommission-101.html
Die von Ihnen angekündigte "MONDLANDUNG" für Europas Industrie
wird eine Bauchlandung.
Mit Personenschaden.
Möglicherweise mit multimillionenfachen Personen-und-Vermögensschäden.
Wenn der JUMBOJET EUROPA abstürzt……
……..Treibstoffmangel.
Und warum ?
Sie alle bei der ARD glauben das Horrorscenario des IPCC.
Ich habe es widerlegt:
Grüne Weihnachten ? Schnee zu Neujahr ?
Kann irgendjemand auf der Welt berechnen
um wieviel Grad es in elf Tagen wärmer oder kälter ist als heute ?
http://www.schottie.de
Gesendet: Samstag, 21. Dezember 2019 um 11:54 Uhr,……………………………. MdEP
Von: "Rainer Schottlaender"
An: "Erik Marquardt"
Betreff: Was für ein Klimaglück der Homo Sapiens hat
https://de.wikipedia.org/wiki/Klimageschichte#/media/Datei:All_palaeotemps_G2.svg
RS => – 12 K in den letzten 500 Mio Jahren….
" Die Klimageschichte beginnt mit der Entstehung der Erde
vor etwa 4,6 Milliarden Jahren.
Im Anfangsstadium der Erde kurz nach der Entstehung
betrug die bodennahe Temperatur etwa 180 °C. .."
RS => 24 K/Mrd a = 110 K/4,6 Mrd a
Vergleiche mit 180 K – heutige 15 K = 165 K
RS => Langsames exponentielles Abfallen der Sonnenaktivität
ergibt ca. – 0,02 K pro 1 Million Jahre
Ziel von Exp 79 war es zu messen, wie die Zugabe einer schwachen Säure
den pH-Wert und das Kalk-Kohlensäure-Gleichgewicht ändert.
Es dauert 3 Tage ( !! ) bis zur Einstellung des CO2-Gleichgewichts :
8 Uhr 35 6511 ppm pH 7,06 (+0,2 pH) 16 C 16/1/20
19 – 00 6580 ppm 18 C 15/1/20
09 – 00 5909 ppm 14 C 15/1/20
19 – 35 5584 ppm 16 C 14/1/20
12 – 30 5385 ppm 16 C 14/1/20
06 Uhr 30 5251 ppm T = 16 C 14/1/20
17 Uhr 25 4130 ppm 18 C 13/1/20
12 – 55 3052 ppm 16 C
10 – 15 2596 ppm 15 C
8 – 25 1862 ppm 15 C
Start bei 1600 ppm pH 6,86 15 C
Es wurde zu Beginn ca. 0,5 cm^3 handelsüblicher Branntweinessig mit 5 % Säure
= ca. 25 mg CH3COOH dem Gleichgewichts-Leitungswasser aus Exp 78 hinzugegeben.
https://de.wikipedia.org/wiki/Essigs%C3%A4ure#Chemische_Eigenschaften
Copyright 1990 – 14. Januar 2020 :
http://www.schottie.de
Betreff: Auswertung Experiment 79 / Start Experiment 80, wissen@russische-botschaft.de, "europamanagement@ec.europa.eu" , glatz@itu.ftz.de, post.pet@bundestag.de, angela.merkel@bundestag.de, mail@bundestag.de, "kreutzmann@bundespressekonferenz.de" , berlin@bundespressekonferenz.de, "internetpostbundesregierung.de" , andrzej.przylebski@msz.gov.pl, BerlinPCO@state.gov, p.stefanov@mediapioneer.com, holger.schacht@protonmail.com, "Allgemein ARD Morgenmagazin" , ard-morgenmagazin@daserste.de, "redaktiontagesspiegel.de" , redaktion@wdr.de, redaktion@welt.de, redaktion@faz.net, dekanat@physik.uni-heidelberg.de, info@physi.uni-heidelberg.de, uwer@Physi.uni-heidelberg.de, stachel@physi.uni-heidelberg.de, dubbers@physi.uni-heidelberg.de, kasang@dkrz.de, "info@dkrz.de" , boettinger@dkrz.de, jana.meyer@dkrz.de, akoertzinger@geomar.de, "sekretariat-me@geomar.de" , info@geomar.de, kmatthes@geomar.de, hosst@geomar.de, mlenz@geomar.de, karin.lochte@awi.de, Ingeborg.Levin@iup.uni-heidelberg.de, ttanhua@geomar.de, nicolas.gruber@env.ethz.ch, "David (Communications Partnerships)" , drfeldman@lbl.gov, "Peter.krothuni-konstanz.de" ,
Gesendet: Donnerstag, 16. Januar 2020 um 15:51 Uhr
Von: "Rainer Schottlaender"
An: EO@ombudsman.europa.eu, georg.arens@bmu.bund.de, gerhard@sabathil.eu, "Erik Marquardt"
Gesendet: Dienstag, 14. Januar 2020 um 07:37 Uhr
Von: "Rainer Schottlaender"
An: Sie, wie üblich ignoriert
Betreff: Experiment 79
Gesendet: Dienstag, 21. Januar 2020 um 17:58 Uhr, post.pet@bundestag.de, angela.merkel@bundestag.de, mail@bundestag.de, "kreutzmann@bundespressekonferenz.de" , berlin@bundespressekonferenz.de, "internetpostbundesregierung.de"
Von: "Rainer Schottlaender"
An: hr-fernsehen@hr.de, fernsehen@br.de, Publikumsservice@mdr.de, fernsehen@ndr.de, zuschauerredaktion@radiobremen.de, service-redaktion@rbb-online.de, zuschauerredaktion@sr-online.de, tv@swr.de, publikumsstelle@wdr.de, feedback.german@dw.de, zuschauer@ard-digital.de, info@3sat.de, kika@kika.de, info@phoenix.de, "europamanagement@ec.europa.eu"
Betreff: an die ARD und an die Bundesregierung
Erinnern Sie sich noch an die Zeit, als alle Welt glaubte,
Spinat würde zehnmal mehr Eisen enthalten als anderes Gemüse ?
Ursache war ein Tippfehler der Kommastelle, der niemandem jahrzehntelang auffiel.
Mir kamen bereits im Jahr 1990 Zweifel an der heute Ihre täglichen Sendungen
beherrschenden Theorie zu CO2.
Ich informierte bereits 1992 Bundeskanzler Helmut Kohl, dass
"… eine Energiewende ein VIELFACHES der Wiedervereinigung kosten wird…"
Aufgrund der Wichtigkeit der Energieversorgung für jeden Bürger Deutschlands
habe ich noch einmal den Einfluss von CO2 auf die Lufttemperatur
und den Meeresspiegel durchgerechnet.
Mein Resultat in Zahlen:
T ( 2300, 1600 ppm ) < T ( heute, 400 ppm) + 1,6 K In einem Satz: Die Menschheit erwartet selbst bei Verbrennung aller abbaubaren Öl-Gas-und-Kohlereserven keineswegs eine "unbewohnbare Erde" (IPCC/NASA) Prüfen Sie mein Resultat und stellen Sie Fragen: http://www.schottie.de
Gesendet: Freitag, 08. Mai 2020 um 08:01 Uhr
Von: "Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de
Cc: mail@bundestag.de, vorzimmer.peta@bundestag.de
Betreff: Beleg-EMail für Bundespräsident Steinmeier
Die richtige Antwort entscheidet die Zukunft Deiner Kinder
Die Welt glaubt weiterhin dem IPCC, der NASA und dem alten Hansen, der sagt, dass es am Äquator um 20 Grad
und an den Polen um 30 Grad wärmer wird …wenn die Menschheit alle Kohle-Gas-und-Ölreserven verbrennt.
Das habe ich geprüft:
https://www.schottie.de/?p=11809
… nach 301 Arbeitsstunden zum Thema Corona : https://www.schottie.de/?p=11874
… Die Überschrift IM MAI IST CORONA VORBEI habe ich übrigens bereits am 14. März veröffentlicht
… 9 Tage vor dem Lockdownwahn der früheren FDJ-Agitatorin Angela Merkel.
… nun in unerledigter existenzieller Sache wieder zum kollektiven Klimawahn:
Bis heute, Freitag den 8. Mai 2020, nach 200 Jahren Industrialisierung,
bemerke ich erstmal einmal nichts Dramatisches.
Weder in Berlin – noch sonstwo auf der Welt.
In den nächsten 200 Jahren wird die Menschheit vermutlich alles verbrennen was wirtschaftlich abbaubar ist.
Bisher waren das 500 GtC … und vermutlich 4000 GtC sind abbaubar.
Im Ruhrgebiet holten wir bisher 10 GtC aus der Erde, es ist noch reichlich Kohle da.
Ein Mehrfaches des bisher Gefördetem.
Weil die Menschen gierig waren haben sie 100 Euro pro Tonne Steinkohle plus Subventionen eingesackt
aber die ausgekohlten Schächte nicht für 10 Euro pro Tonne wieder aufgefüllt
sondern auch dieses Geld lieber verkonsumiert.
Deshalb sackte das komplette Ruhrgebiet um viele Meter ab.
Die Schulden sind geblieben – die Kohle ist weg – die Arbeitsplätze auch.
Nach uns die Sintflut.
Wie bei der Rente … dank Norbert Blüm … Info hier :
https://www.schottie.de/?p=11941#comment-130557
Der Bundespräsident prahlte am 18.12.2019 mit dem letzten geförderten Stück Ruhrkohle.
Der Fisch beginnt am Kopf zu stinken.
Erinnern Sie sich an 1918, 1923, 1945 …
So wird es kommen – wenn wir sie lassen.
Es liegt auch ein bischen an Dir.
https://de.wikipedia.org/wiki/Kohlenstoffzyklus
"Häufigste Elemente der Erdkruste: Sauerstoff 49 %, Eisen 19 %, Silicium 14 %, Magnesium 12,5 %
(Kohlenstoff dagegen nur 0,099 %)
Die globale Kohlenstoffmenge beträgt 75 Millionen Gt.
Terrestrische Ökosysteme enthalten 800 Gt C, marine 3 Gt C in der Biosphäre,
was insgesamt einem Anteil von 0,001 % am globalen Gesamtkohlenstoff entspricht.
Kohle: Kohlelagerstätten entstanden aus den Waldmooren der Karbonzeit vor etwa 359 bis 299 Millionen Jahren.."
Wenn 60 Millionen Jahre lang 100.000 Tonnen C/a sedimentieren sind das 6000 GtC.
Wo kamen diese 100.000 tC/a her ?
Wie warm war es damals, wenn man etwa -0,01 K (?)
pro Jahrmillion wegen nachlassender Sonnanaktivität bedenkt ?
Wieviel CO2 war damals in der Atmosphäre ?
Wie lebte es sich so damals im Karbon ?
Zur Erwärmung der Erdatmosphäre durch CO2 Von schotti am 30. November 2019 Glaubt man den täglichen Nachrichten, dann bedroht eine globale Erwärmung die Menschheit. Dafür sei das Treibhausgas CO2 hauptverantwortlich. Klimaskeptiker bezweifeln, dass der Temperatur-Anstieg menschengemacht ist…
Zur Erwärmung der Erdatmosphäre durch CO2 Copyright 1990-2020: Schottie.de
Kohle 93 % = 7300 Mrd t SKE der 1972 bekannten Brennstoffvorräte der Welt
Erdöl 4 % = 350 Mrd t SKE
Erdgas 3 % = 233 Mrd t SKE
Quelle: Kleine Enzyklopädie Technik
1976 VEB Bibliografisches Institut Leipzig
Ich rechne hier mit 4000 Mrd t SKE:
https://www.schottie.de/?p=11809
Die Ausdehnung von Wald- und Sumpflandschaften erreichte in der „Steinkohlenzeit" des Karbon ein neues Maximum. Das globale Klima besaß anfangs subtropischen Charakter, kühlte jedoch bis zum Ende der Epoche stetig ab und sank zum Schluss deutlich unter das gegenwärtige Niveau.
Das Karbon begann vor etwa 358,9 Millionen Jahren und endete vor etwa 298,9 Millionen Jahren…"
https://de.wikipedia.org/wiki/Karbon
6000 GtC Steinkohle = 6.000.000.000.000 tC / 60.000.000 Jahre = 100.000 Tonnen Steinkohle sedimentierten pro Jahr.
Jede einzelne Tonne war vor ihrer Beerdigung in der Atmosphäre.
Und/oder im Ozean.
Heute stehen 400 ppm CO2 = 800 GtC
im Gleichgewicht mit 40.000 GtC ozeanischem Kohlenstoff Ca(HCO3)2.
93 % des fossilen Kohlenstoffs sollen als Kohle gebunden sein, nur 4 % als Erdöl und nur 3 % als Erdgas.
Bisher hat die Menschheit 500 GtC Kohle, Das und Öl verbrannt.
Ca. 4000 – 6000 GtC sind vermutlich abbaubar, zB für unter 200 Dollar pro Tonne C.
10 Mrd t wurden in den letzten 200 Jahren im Ruhgebiet abgebaut.
Ca. 100 Mrd t liegen noch ungenutzt unter der Erde.
Wegen Gier wurden die ausgekohlten Schächte nicht wieder aufgefüllt,
weswegen das gesamte Ruhrgebiet um mehrere Meter absackte.
Waren damals im Karbon die von Wiki angegebenen 800 ppm CO2 in der Erdatmosphäre ?
Bei fast derselben Temperatur wie heute ?
Wie kann es dann "am Äquator 20 Grad und an den Polen 30 Grad wärmer werden,
wenn die Menschheit allen fossilen Kohlenstoff verbrennt ?"
Das ist die herrschende Lehrmeinung von NASA, Hansen und dem IPCC.
https://www.general-anzeiger-bonn.de/news/politik/klimaforscher-der-planet-waere-unregierbar_aid-43559349
https://de.wikipedia.org/wiki/Galoppierender_Treibhauseffekt
Meines Erachtens ist das alles falsch.
Der Treibhauseffekt auf Planet Venus entseht durch die dortige 90 bar Atmosphäre.
Ein "dicker Pullover" wärmt besser.
Ich habe auch Mars und Jupiter nachgeprüft und kann den Temperaturverlauf dort erklären.
Interessiert zwar niemanden
Aber vielleicht den einen oder anderen Leser meines blogs:
Die jungen Menschen in Europa stellen die richtige Frage.
Nach ihrer Zukunft.
Ich frage jeden einzelnen Mitbürger.
Jetzt und hier DICH:
MAXIMAL 1,6 GRAD GLOBALE ERWÄRMUNG
https://www.schottie.de/?p=11809
Richtig oder falsch ?
Hallo schottie,
ich heiße Ferenc und
wir haben etwa zur gleichen Zeit Physik studiert.
Für Klima habe ich mich erst seit Greta angefangen zu interessieren.
(Sie ist halt sooo sympatisch)
Mein Enkelsohn hatte mir im Sommer 2019 erzählt, dass die Erde sich in den nächsten Jahren um 5°C erwärmen würde, daher muß er zu Klima Demos, muss zum Vegetarier werden …
Wie ich erfahren musste, weiß er all das von seinem Ethik Lehrer.
All das hat mich fürs erste ein bisschen mulmig gemacht und mein Interesse fürs Klima geweckt.
Ich wollte mir ein eigenes Bild machen.
Gerade wollte ich selber eine Berechnung für die Erde und zum Qualitätscheck über den Venus anstellen.
So bin auf Ihrer (deiner ?) Seite Dank unserem besten Freund Google gelandet.
Meine erste Frage: Was ist die Abstrahlhöhe der Erde ?
Ich habe etwa 5Km in Erinnerung, kann das aber im Moment nirgendwo finden.
Ich stelle halt an Google die falschen Fragen.
Viele Grüße
Ferenc
Warm air rises up.
In numbers: mgdh + mCpdT = 0 (conservation of energy) ===> dT/dh = – g/Cp
This is the basic law that rules every planet atmosphere in the universe.
Like S = g/2 x t^2 rules how a stone falls.
In the first approximation.
Without friction, water vapor influences, radiation and other effects.
I have needed a while before I have understood the small influence of radition on T(CO2,h).
The first experiment to learn more I did June 26, 1992 :
On my girl friends balcony I have put a second glass cover on an aquarium.
Simulating what happenes if atmospheric CO2 content doubles from todays 400 ppm to 800 ppm.
Results published in my "book" PRIMA KLIMA, part 1, page 48.
Than a few years later I have independently reinvented and performed in my lab and in my garden an easy experiment which Prof. Robert Wood did already 112 years ago.
https://de.wikipedia.org/wiki/Robert_Williams_Wood
↑ Wood, R. W.: Note on the Theory of the Greenhouse. In: Philosophical Magazine. 17, 1909, S. 319–320
Wood has used in 1909 a salt glass plate, transparent for infrared radiation
I have used in 1995 a thin polyethylene household foil for 1 Euro from my supermarket.
Nahle did it in 2011 with more time effort and money better than I with the same result:
https://www.biocab.org/Experimente_zum_Treibhauseffekt.pdf
After publishing my 37 Thesis for CO2 in January 2011
I have looked in 2019 again a little bit deeper into the theory:
Um zu verstehen wie CO2 die Temperatur beeinflusst beginnen wir bei Null:
Bild 1 zeigt die hypothetische 0 ppm CO2 Linie – – – – – über Guam
Bild 3 zeigt bei 1,3,5 und sieben Luftmassen Gegenstrahlung und Absorption:
Ich betrachte und vermesse Fig.24:
1600 ppm CO2-Luft verschiebt die Absorption dieser 4,3 µm Bande in Fig.24
maximal um 2 mm x 4 mm = 8 mm2 bei einer Gesamtfläche von 15 x 120 = 1800 mm2
Dadurch zu erwartendes dT = dU/U x T/4 = 8/1800 x 300 K/4 = aufgerundet 0,4 K
Die Messung erfolgte mittags. Nachts liegt der Wert darunter.
Berechnung des Beitrages der 15 µm Bande zur globalen Erwärmung:
Hierzu Bild 2: Infrarotspektrum der Erde gemessen vom Satelliten Nimbus 4 https://de.wikipedia.org/wiki/Nimbus-Programm
Bei 667 cm^-1 misst der Satellit …
Learn more here: https://www.schottie.de/?p=11809
Saldo: +0,4 K + 1,5 K – 0,3 K = + 1,6 K
maximal global warming because of CO2 even if we burn all fossile C.
Am I right or wrong ?
Gesendet: Samstag, 15. Mai 2021 um 11:45 Uhr, sfurfari@gmail.com
Von: "Rainer Schottlaender"
An: "Gerhard Sabathil"
Betreff: Aw: Re: Sehr geehrte Professoren Furfari und Sabathil
First things first.
After a terrible week with gastritis my power comes back.
I just did 7 x 1 slow rounds in our wonderful forest stadium here,
watched the clouds and thought again about my life and our atmosphere.
https://youtu.be/OwqIy8Ikv-c
I have listened these 5 minutes and agree with every single word of Prof. Richard Lindzen.
Most of this I have already known and published in the 1990`s : www.schottie.de/?p=46
Before we look deeper into the physics let me try a social experiment:
I imagine my audience is Greta Thunberg and 50.000 of her fanatic fans
in the Wembley stadium.
How would I argue ?
If I get the microphone for one minute:
"Each of you here is asking the right question.
If the earth becomes uninhabitable because of CO2 then we have to act immediately.
Even faster and more drastic than you ask.
But consider the consequences before you act.
For your own life.
What if you are wrong?
If I'm wrong, I'll give back my physics diploma.
Do you do the same with your doctorate, Mrs. Merkel?
The consequences of a world without the use of fossil carbon and nuclear energy
are so drastic
that this question needs to be answered without any doubt:
https://www.schottie.de/?p=11809
Gesendet: Samstag, 15. Mai 2021 um 09:31 Uhr, "Schottlaender Rainer"
Von: "Gerhard Sabathil"
An: "Samuel Furfari"
Betreff: Re: Sehr geehrte Professoren Furfari und Sabathil
Merci cher Sam, voila
G
Von meinem iPhone gesendet
Am 15.05.2021 um 08:40 schrieb Samuel Furfari:
Dear Gerhard,
Could you please transfer this email to Mr Rainer Schottlaender.
Dear M. Schottlaender,
Thank you very much for your kind reaction and the time you consecrated to the analyse of Prof Geuskens paper.
I deduce that we are broadly in agreement. Geuskens says that there is no greenhouse effect of the CO₂, and you are saying that its impact is ten times less than what the majority of people believe. Your position is similar to that of Prof Richard Lindzen. This prestigious professor of MIT resigned few years ago as a lead author of IPCC because he found that there is too much exaggeration. I invite you (and specially Gerhard to look at this recent video in which he explains his position https://youtu.be/OwqIy8Ikv-c).
Anyway, your /Lindzen position or Geuskens one leads to the same conclusion : we are destroying our economy for something that it is of any value.
I am regularly in contact with Patrick Moore, one of the founders of Greenpeace, because we share the same position.
I did not know the nice story of the spinach…. Thanks.
I am particularly worried that German people stubbornly want to do more to reduce CO₂ to the point to kill its own car industry. We will end up importing electrical cars from China and they will dominate the world. As a convinced EUer I would like to see the common sense to return.
Best regards,
Samuel Furfari
Les problèmes d'aujourd'hui doivent être traités avec les solutions d'aujourd'hui qui ont été conçues par les ingénieurs ; les problèmes de demain seront résolus avec les solutions de demain qui seront également conçues par les ingénieurs., a écrit :
Le 14 mai 2021 à 23:52 +0200, Gerhard Sabathil
Von meinem iPhone gesendet
Anfang der weitergeleiteten Nachricht:
Von: Rainer Schottlaender
Datum: 14. Mai 2021 um 11:47:07 MESZ
An: Gerhard Sabathil
Kopie: Martin Regehly
Betreff: Sehr geehrte Professoren Furfari und Sabathil
Ich kommentiere hier in dieser EMail die mir durch Sie
heute bekannt gewordene Arbeit von Georges Geuskens.
Anthropogene globale Erwärmung
14. Februar 2019atmosphäre und CO2, Klima, enge WirkungAmosphäre, CO2 Georges Geuskens
Das Klima kann sich wie immer ändern und wird dies auch weiterhin unter dem Einfluss natürlicher Variablen tun. Können menschliche Aktivitäten einen Einfluss haben, wie es die Theorie der anthropogenen globalen Erwärmung behauptet? Diese Theorie basiert auf der Existenz eines hypothetischen Treibhauseffekts, der als Strahlungsphänomen definiert ist, das durch Gase wie Wasserdampf oder CO2 verursacht wird, die einen Teil der von der Erde emittierten Infrarotstrahlung absorbieren und dann in alle Richtungen und nach innen wieder abgeben insbesondere in Richtung der Erdoberfläche, deren Temperatur daher höher wäre als ohne Infrarot absorbierendes Gas. Der Treibhauseffekt würde sich daher im Wesentlichen aus der Emission von Fluoreszenzstrahlung im Infrarotbereich durch CO2-Moleküle ergeben [1]. Diese Definition ist klar und wissenschaftlich gültig, da sie dem von Karl Popper definierten Prinzip der Widerlegbarkeit entspricht. Wir werden es im Lichte gut etablierter physikalischer Theorien und bekannter experimenteller Fakten untersuchen.
1. CO2 in den unteren atmosphärischen Schichten
Vergessen wir zunächst das Klima und betrachten eine undurchsichtige Box, die eine bestimmte Menge trockener Luft bei 15 ° C und dem Druck einer Atmosphäre enthält und vor jeglicher äußeren Strahlung geschützt ist. In dieser Box sind 78% der Moleküle N2-Stickstoffmoleküle und 21% O2-Sauerstoffmoleküle. Der dritte Bestandteil in der Reihenfolge der Häufigkeit ist Argon Ar (etwa 1% der Moleküle). CO2-Moleküle sind nur zu etwa 0,04% beteiligt. Alle diese Moleküle haben praktisch keine Wechselwirkung zwischen ihnen, außer dass sie bei ständiger Bewegung bei Schocks, von denen die meisten elastisch sind (unter Erhaltung der kinetischen Energie), miteinander kollidieren.
1a) Übersetzungsenergie
Die kinetische Theorie der Gase ermöglicht es zu berechnen, dass bei einer Temperatur von 15 ° C die Luftmoleküle durch Translationsgeschwindigkeiten in der Größenordnung von 500 m pro Sekunde angetrieben werden und dass beim Druck einer Atmosphäre jeweils mehrere Milliarden Kollisionen auftreten pro Sekunde. Diese Moleküle weisen eine breite Geschwindigkeitsverteilung auf, die gemäß dem Maxwell-Boltzmann-Gesetz eine Funktion der Temperatur ist (Abb. 1). Die durchschnittliche kinetische Energie der zweiatomigen Moleküle N2 und O2 kann berechnet werden und beträgt Em = 5/2 k T (wobei k die Boltzmann-Konstante und T die Temperatur in Kelvin ist).
RS: All correct
1 Maxwell-Boltzmann-Geschwindigkeitsverteilungsgesetz
1b) Schwingungsenergie
Luftmoleküle bewegen sich nicht nur in der Translation. Wenn sie genügend Energie haben, können sie auch mit schnellen und periodischen Variationen in den Längen oder Winkeln ihrer interatomaren Bindungen schwingen. Die zweiatomigen Moleküle N2 und O2 sind sehr starr und vibrieren bei 15 ° C kaum. Im Gegensatz dazu können sich triatomische CO2-Moleküle, die im Grundzustand O = C = O linear sind, beim Vibrieren leicht verformen und eckig werden. Jede Schwingungsfrequenz ist mit einer Energie verbunden, und die Quantentheorie lehrt uns, dass nicht alle Schwingungsfrequenzen zulässig sind. Es existieren nur bestimmte Energieniveaus, deren Energie durch Absorptionsspektroskopie im Infrarot- oder Raman-Bereich experimentell bestimmt werden kann. Somit kann die mit der Verformungsschwingung von CO2 verbundene Energie aus der Absorptionsbande berechnet werden, die bei 15 um im Infrarotspektrum des Moleküls detektiert wird, dank der Beziehung Ev = hc / λ (wobei h die Konstante von Planck ist, c die Geschwindigkeit von Licht und λ die Wellenlänge der absorbierten Strahlung, in diesem Fall 15 um). Dieser Wert ist nur 30% höher als Em, die durchschnittliche kinetische Energie der umgebenden Moleküle N2 und O2, die im vorherigen Absatz erwähnt wurde. Viele dieser Moleküle haben jedoch eine überdurchschnittlich hohe Geschwindigkeit, wie in Abb. 1 gezeigt. 1 (die Durchschnittsgeschwindigkeit liegt sehr nahe am Maximum der Geschwindigkeitsverteilungskurve) und damit auch eine überdurchschnittlich hohe kinetische Energie Ec.
RS: All correct
1c) Umwandlung von Translationsenergie in Schwingungsenergie und umgekehrt
In Abwesenheit einer externen Strahlungsquelle kann die Energie, die zur Anregung der CO2-Schwingung erforderlich ist, nur aus der thermischen Bewegung der Umgebung stammen. Die Quantifizierung der Energie greift nicht auf der Ebene der Translationsbewegungen ein, und die kinetischen Translationsenergien Ec = mv2 / 2 haben eine breite kontinuierliche Verteilung ähnlich der in Abb. 1 dargestellten. 1. Die diesen Kurven entsprechende mathematische Funktion ermöglicht es zu berechnen, dass bei 15 ° C mehr als 40% der N2- und O2-Moleküle eine kinetische Energie Ec haben, die größer ist als die Energie Ev des niedrigsten Schwingungsniveaus der CO2-Moleküle. Sie können es daher während einer unelastischen Kollision (ohne Erhaltung der kinetischen Energie) auf dieses Niveau bringen. Unter diesen Bedingungen erfolgt eine Umwandlung eines Bruchteils ∆ der translatorischen kinetischen Energie der N2- oder O2-Moleküle in die Schwingungsenergie eines Bruchteils der CO2-Moleküle:
∆Ec (Translation) von N2 + CO2 → ∆Ev (Vibration) von CO2 + N2 (1)
Es sind offensichtlich nicht immer dieselben CO2-Moleküle, die sich in einem Schwingungszustand befinden, da diese Umwandlung reversibel ist und die Moleküle innerhalb weniger Millisekunden deaktiviert werden, um bei neuen Schocks mit den umgebenden Molekülen in den Grundzustand zurückzukehren, die daher vorübergehend eine Zunahme annehmen in translatorischer kinetischer Energie:
∆Ev (vibration) de CO2 + N2 → ∆Ec (translation) de N2 + CO2 (2)
RS: It seems all correct, mir fehlt etwas Wissen hierzu
Es besteht daher ein dynamisches Gleichgewicht, das mit den Reaktionen (1) und (2) verbunden ist, die zueinander invers sind. Dieses Gleichgewicht hängt nur von Temperatur und Druck ab (durch die Verteilung der Energien und die Anzahl der Schocks zwischen den Molekülen). Obwohl nicht immer dieselben CO2-Moleküle schwingen, bleibt der Anteil der Moleküle in einem Schwingungszustand bei einer bestimmten Temperatur und einem bestimmten Druck konstant (etwa 40% bei 15 ° C unter dem Druck einer Atmosphäre). Dieses Gleichgewicht wird nicht verändert, wenn zusätzlich einige CO2-Moleküle angeregt werden, indem ein Teil der von der Erde emittierten Infrarotstrahlung absorbiert wird. Es kann daher geschlossen werden, dass die Deaktivierung von CO2-Molekülen nicht mit der Emission von Strahlung erfolgt. Der Grund ist, dass bei Drücken nahe einer Atmosphäre die Fluoreszenz mit der Deaktivierung der Kollision nur um angeregte Zustände mit sehr kurzer Lebensdauer (10-9 bis 10-7 s) konkurrieren kann, die auftreten können. Deaktivieren Sie sie durch Fluoreszenz vor einer ausreichenden Anzahl von Kollisionen mit umgebenden Molekülen auftreten. Bei einer Lebensdauer des niedrigsten angeregten CO2-Zustands von 0,64 s [2] treten jedoch Millionen von Kollisionen auf, bevor Strahlung emittiert werden kann. Die Hypothese des Treibhauseffekts ist daher ohne theoretische Grundlage.
RS: I disagree with the last sentence
Zusätzlicher Hinweis basierend auf experimentellen Ergebnissen
Die Umwandlung von Schwingungsenergie in Translationsenergie (V → T) und Translationsenergie in Schwingungsenergie (T → V) wie in den Reaktionen (1) und (2) ist ein bekanntes Phänomen, dessen Untersuchung sich dank der Fortschritte in der Lasertechnologie entwickelt hat selektiv unterschiedliche Schwingungszustände zu erhalten [3].
Insbesondere die Umwandlung von Schwingungsenergie in Translationsenergie (V → T) wurde bei laserangeregten CO2-Molekülen im niedrigsten Schwingungszustand untersucht. Die Reaktionsgeschwindigkeitskonstanten:
CO2 * + N2 (oder O2) → CO2 + N2 (oder O2)
wurden zwischen 300 und 140 K gemessen [4]. Sie liegen in der Größenordnung von 105-mal niedriger als diejenigen, die auf der Grundlage der Anzahl der Kollisionen (mehrere Milliarden pro Sekunde) vorhergesagt wurden, da sie nur aus unelastischen Kollisionen resultieren, die nur 0,001% der Gesamtzahl der Kollisionen ausmachen.
Andererseits wurde auch die Umwandlung von Translationsenergie in Schwingungsenergie (T → V) im Fall von CO2 untersucht. In Höhen in der Größenordnung von 100 km kann die translatorische kinetische Energie von Sauerstoffatomen auf CO2-Moleküle übertragen und in Schwingungsenergie umgewandelt werden [5]:
O + CO2 → O + CO2 *
Das Phänomen wurde durch Nachweis der Fluoreszenz (Strahlungsdeaktivierung) von CO2-Molekülen mit Strahlungsemission der Wellenlänge λ = 15 µm demonstriert:
CO2 * → CO2 + hc / λ
In diesen Höhen ist der atmosphärische Druck so niedrig, dass die Gesamtzahl der Kollisionen zwischen Molekülen nur etwa 1000 pro Sekunde beträgt.
Ein Teil der angeregten CO2-Moleküle kann dann mit der Emission von Strahlung deaktiviert werden, bevor eine unelastische Kollision mit den umgebenden Molekülen auftritt. Dies ist in den unteren atmosphärischen Schichten nicht der Fall, in denen die Emission von Fluoreszenzstrahlung von CO2 nie beobachtet wurde. Die von Befürwortern der anthropogenen globalen Erwärmung angeführte Hypothese des Treibhauseffekts ist daher weder theoretisch noch experimentell gerechtfertigt.
RS: I do not know if 0,001 % is correct.
2. Die Energiebilanz der Erde
Um den Anteil der Wärmestrahlung von der Erde abzuschätzen, der von CO2 absorbiert werden könnte, muss die Energiebilanz der Erde berücksichtigt werden, die auf der Idee basiert, dass die Erde zur Aufrechterhaltung einer konstanten Temperatur die von verschiedenen empfangene Energie abführen muss Mechanismen der Sonne. Das am häufigsten zitierte Modell ist das von der NASA vorgeschlagene (Abb. 2).
Energiebilanz der Erde nach NASA
Nach diesem Bericht würden 30% der von der Erde am oberen Ende der Atmosphäre empfangenen Energie von den Wolken, der Atmosphäre und der Erdoberfläche gemäß einer Albedo von 0,3 reflektiert. Die Atmosphäre und die Wolken würden zusätzlich 19% der durchgelassenen Sonnenstrahlung absorbieren und letztendlich würden nur 51% von Kontinenten und Ozeanen absorbiert. Diese Energie würde dann durch drei unterschiedliche Mechanismen abgeführt: Verdunstung des Meerwassers (23%), Luftkonvektion (7%) und Wärmestrahlung (21%). Zunächst ist zu beachten, dass die in Fig. 2 dargestellte Waage keine "Rückstrahlung" zeigt, die mit einem möglichen Treibhauseffekt verbunden ist. Nur ein kleiner Teil der vom Satelliten erfassten Strahlung kommt direkt von der Erdoberfläche (dünner roter Pfeil rechts in Abb. 2), da sie in der Zone atmosphärischer Transparenz zwischen 8 und 13 µm emittiert wird (Abb. 3). Durch Integration der Planckschen Gleichung für einen schwarzen Körper bei 15 ° C im Bereich von 8 bis 13 µm berechnen wir, dass 30% der Erdwärmestrahlung in dieser Zone atmosphärischer Transparenz emittiert werden. 6% der Gesamtenergie, die von der Sonne am oberen Rand der Erdatmosphäre empfangen wird. Der Rest der von der Erde emittierten Wärmestrahlung wird von verschiedenen atmosphärischen Bestandteilen (Abb. 3) absorbiert, hauptsächlich Wasserdampf, aber auch CO2. Unabhängig vom Energiedissipationsmechanismus auf der Höhe der Erdoberfläche muss all diese Energie in der Höhe in Strahlung umgewandelt werden, da dies der einzige Mechanismus ist, mit dem sie aus dem Erdsystem evakuiert werden kann (großer roter Pfeil in Abb. 2).
RS : All correct
Übertragung von Infrarotstrahlung durch die Erdatmosphäre (Transparenzbereiche erscheinen blau, insbesondere zwischen 8 und 13 µm)
Die in der Energiebilanz der NASA genannten Anteile sind oft nur Schätzungen. Sie sind auch ziemlich überraschend, da Konvektion im Allgemeinen der vorherrschende Mechanismus für Objekte bei Umgebungstemperatur und -druck ist, während Wärmestrahlung nur bei hoher Temperatur signifikant wird.
Aus dieser Perspektive sind Sorokhtin und Mitarbeiter [5] der Ansicht, dass die Konvektion bei 34% tatsächlich der vorherrschende Mechanismus ist, während die Wärmestrahlung nur bei 4% und die Verdunstung des Meerwassers bei 13% interveniert.
Es besteht daher große Unsicherheit über die relative Bedeutung dieser drei Mechanismen.
RS: Yes. Study my work about this :
dT/dh = – g/Cp controls T in planetary atmospheres.
In this well known formulae you find just Cp (about 1 J/gK),
nothing about the radiation of traces gases.
Auf der Höhe der Erdumlaufbahn erhält jeder Quadratmeter senkrecht zur Sonnenstrahlung im Jahresdurchschnitt eine Leistung von 1368 W, dies ist die "Sonnenkonstante". Der Durchschnittswert von 342 W m-2 am oberen Rand der Atmosphäre basiert auf der Idee, dass jeder Quadratmeter der Erdoberfläche kontinuierlich ein Viertel von 1368 W erhält, da die Erde nur Sonnenstrahlung auf einer Oberfläche abfängt, die der von entspricht eine Scheibe mit dem gleichen Radius. Dieser Wert wird nicht gemessen, sondern unter der Annahme einer gleichmäßigen Energieverteilung über die gesamte Erdoberfläche berechnet, ohne dass entweder eine unbeleuchtete Halbkugel oder eine Änderung des Breitengrads berücksichtigt werden. Daher wird es sicherlich überschätzt. Wenn die Energieverteilung gleichmäßig wäre, gäbe es außerdem keine Jahreszeiten, keine See- oder Luftströmungen, die jedoch Elemente des Klimas bestimmen. Dieser ungefähre Wert wird jedoch im Allgemeinen angenommen, da ein korrekter Wert unter Berücksichtigung der Rotationsgeschwindigkeit der Erde und der Neigung ihrer Rotationsachse zu unüberwindlichen Berechnungsschwierigkeiten führen würde. Wenn man der Erde eine Albedo von 0,3 zuschreibt, die nicht nur die von der Erdoberfläche und der Atmosphäre, sondern auch und hauptsächlich von den Wolken reflektierte Energie beinhaltet, würde die tatsächlich von der Erdoberfläche empfangene Strahlung auf 70% von 342 reduziert W m-2 oder ungefähr 240 W m-2. In großen Höhen erfassen Satelliten effektiv eine durchschnittliche Strahlung von 240 W m-2 mit einer Differenz in der Größenordnung von 50 W m-2 zwischen den Polen und dem Äquator. Diese durchschnittliche Strahlung stammt hauptsächlich aus den oberen Schichten der Atmosphäre bei Temperaturen, die weit unter denen der Erdoberfläche liegen, und es kann auf der Grundlage der Stefan-Boltzmann-Formel nicht abgeleitet werden, dass die Erdoberfläche eine Temperatur von – 18 ° haben sollte C (siehe hier).
RS: Again: Radiation rules just a small part.
Gravity rules T-surface (Example: Venus, Mars, Earth, Jupiter):
dT/dh = – g/Cp
Wenn wir die Erde bei 15 ° C als schwarzen Körper betrachten, können wir nach der Planckschen Gleichung (siehe hier) berechnen, dass 95% des Emissionsspektrums zwischen 5 und 40 µm liegen, und das Wiener Gesetz sagt voraus, dass die emittierte Strahlung ein Maximum aufweisen sollte Intensität bei 10 um. CO2 zeigt eine Absorptionsbande im Bereich der Wärmestrahlung der Erde. Es ist in Abb. 2 dargestellt. 4 für einen CO2-Gehalt von 357 ppm (0,0357%) in Gegenwart von 2,6% Wasserdampf, Bedingungen entsprechend der atmosphärischen Zusammensetzung im Jahr 1993.
RS: All numbers correct
4 Infrarotabsorptionsspektrum von CO2
Die bei 15 um zentrierte Absorptionsbande ermöglicht es, das Molekül bei seiner niedrigsten Schwingungsstufe anzuregen, die eine Winkelverformung beinhaltet. Die P- und R-Zweige sind auf das Vorhandensein von Rotationsunterstufen für jedes Schwingungsniveau (grundlegend und angeregt) zurückzuführen. Durch Integration der Planck-Gleichung von 14 bis 16 µm, dem Absorptionsbereich von CO2, wird berechnet, dass 9,3% der Wärmestrahlung der Erde in diesem Wellenlängenintervall emittiert werden. Letztendlich konnte CO2 unabhängig von seinem Absorptionskoeffizienten höchstens 9,3% der Wärmestrahlung von der Erde absorbieren (was laut NASA 21% der von der Sonne oben in der Atmosphäre empfangenen Gesamtenergie entspricht) oder etwas weniger als 2% von 342 W m & supmin; ², also ungefähr 7 W m & supmin; ². Für Sorokhtin und Mitarbeiter [5], die Wärmestrahlung der Erde, die nur 4% der von der Sonne empfangenen Gesamtenergie ausmacht, würde das CO2 daher höchstens etwas weniger als 0,4% von 342 W m-2 oder etwa 1,3 W absorbieren m-2.
RS: CO2 increase changes just the flanken at 14 and 16 um.
I have estimated this : https://www.schottie.de/?p=11809
CO2-Moleküle, die durch Absorption eines Teils der Wärmestrahlung der Erde zu einem Schwingungszustand angeregt werden, werden innerhalb von Mikrosekunden durch Kollisionen mit umgebenden Molekülen, hauptsächlich N2 und O2, deaktiviert. Unter diesen Bedingungen wird die Schwingungsenergie von CO2 gemäß der in Absatz 1c genannten Reaktion (2) in kinetische Translationsenergie der N2- oder O2-Moleküle umgewandelt. Obwohl die Absorption von Wärmestrahlung von der Erde zwischen 14 und 16 µm durch die CO2-Moleküle selektiv ist, wird diese überschüssige Energie nach mehreren Kollisionen auf alle umgebenden Moleküle verteilt. Insgesamt werden nach Angaben der Autoren 0,4% oder 2% der von der Sonne am oberen Ende der Erdatmosphäre empfangenen Energie in Konvektionsbewegungen umgewandelt, was sich nachteilig auf die Intensität der Wärmestrahlung auswirkt, von der ein Teil von CO2 absorbiert wird . Das Vorhandensein von CO2 in der Atmosphäre verändert daher nicht die Gesamtenergiebilanz der Erde, sondern nur die relative Bedeutung der verschiedenen Mechanismen der Ableitung der von der Sonne empfangenen Energie. Dies kann keinen Einfluss auf die „durchschnittliche globale" Temperatur der Erdoberfläche haben.
RS: Not fully correct, there is an influence.
I have measured this small effect: https://www.schottie.de/?p=87
This has to be more studied.
3. Einfluss von CO2
Könnte sich die Umwandlung der Schwingungsenergie von CO2 in translatorische kinetische Energie der Moleküle von N2 und O2 in Abwesenheit eines Treibhauseffekts auf die Temperatur der unteren Schichten der Atmosphäre auswirken? Um die Bedeutung eines solchen Effekts abzuschätzen, müsste man das Luftvolumen kennen, in dem diese Energie abgeführt wird. Verwendung der Beer-Lambert-Beziehung mit Io = Einfallsintensität und I = Durchlässigkeitsintensität:
log Io / I = A C L.
und durch Einführung von Werten A = 20,2 m2 / mol für den molaren Absorptionskoeffizienten von CO2 [7] und C = 1,78 10-2 mol m-3 (für 0,04 Vol .-% CO2) stellen wir fest, dass log Io / I gleich ist bis 3 (99,9% Absorption) für eine atmosphärische Dicke L = 8 m. Wenn wir die Anzahl der Moleküle in einer Luftsäule mit einer Höhe von 8 m und einem Volumen von 8 m3 kennen, in der 1,3 oder 7 W abgeführt werden (laut den Autoren), stellen wir fest, dass die durchschnittliche kinetische Energie Em der Moleküle N2 und O2, berechnet in Absatz 1a würde nur in einer Sekunde um etwa 0,0001% zunehmen. Dieser Wert wird nur zum Einstellen einer Größenordnung verwendet, da sich im Laufe der Zeit offensichtlich keine kinetische Energie ansammelt, da bereits ein großer Konvektionsstrom vorhanden ist. Der bereits in den unteren atmosphärischen Schichten vorhandene Temperaturgradient wird daher durch das Vorhandensein von CO2 nicht beeinflusst.
RS : I cannot verify this but agree that convection rules T (h).
Der verwendete molare Absorptionskoeffizient entspricht nur dem Q-Zweig, dem wichtigsten des Absorptionsspektrums (Abb. 4). Für die P- und R-Zweige, deren Absorptionskoeffizienten ungefähr 10-mal niedriger sind, würde die Absorption von 99,9% der Wärmestrahlung von der Erde eine atmosphärische Dicke erfordern, die ungefähr 10-mal größer ist, und die Energieübertragung findet ungefähr über eine Anzahl von Molekülen statt 10 mal größer mit proportional reduzierter Wirkung. Es ist auch zu beachten, dass diese Schlussfolgerungen für das gesamte in der Atmosphäre vorhandene CO2 (0,04%) gelten, unabhängig davon, ob es natürlichen oder menschlichen Ursprungs ist. Viele neuere Studien zeigen jedoch, dass der CO2-Gehalt anthropogenen Ursprungs nur etwa 5% beträgt (siehe hier).
RS: The best measure for global warming is the rise of the sea level:
" 7. In diesen 200 Jahren stieg die Temperatur lokal unterschiedlich angeblich um etwa ein Grad und der Meeresspiegel um 25 cm. Der menschliche Anteil daran war einige ZENTImeter…" https://www.schottie.de/?p=46
4. Fazit
Aus dieser Präsentation können wir schließen, dass:
1 ° Der Treibhauseffekt, der sich aus der Strahlungsdeaktivierung (Fluoreszenz) von Molekülen ergeben würde, die einen Teil der Wärmestrahlung der Erde absorbiert haben, kann auf der Ebene der unteren atmosphärischen Schichten nicht existieren.
2 ° Auf der Ebene der unteren atmosphärischen Schichten werden die Moleküle, die einen Teil der Wärmestrahlung der Erde absorbiert haben, durch Kollisionen mit den umgebenden Molekülen, hauptsächlich N2 und O2, deaktiviert.
3 ° Die Umwandlung der Schwingungsenergie der CO2-Moleküle in die Translationsenergie der umgebenden Moleküle verändert die Gesamtenergiebilanz der Erde nicht.
4 ° CO2 kann in keiner Weise zur Erwärmung der Erdoberfläche oder der unteren atmosphärischen Schichten beitragen.
5 ° Die Theorie der anthropogenen globalen Erwärmung, die auf dem Vorhandensein eines Treibhauseffekts beruht, hat keine theoretische oder experimentelle Rechtfertigung.
RS :
Stop !:
I hope my estimation max + 1,6 K is correct:
https://www.schottie.de/?p=11809
If not I give my diploma back.
——————————————————————–
Dear Prof. Furfari:
I agree with you that we are destroying our economy with an "Energiewende/energy turn… without nuclear energy"
(IPCC, NASA,UNO,Merkel …)
You are a little bit wrong regarding the TREIBHAUSEFFEKT.
I hope you can digest my constructive critics and tell me my mistakes.
There is a small influence of CO2, O3 and CH4 on the temperature.
But it seems this effect is overestimated by a factor 10.
You learn more if you think in detail and thoroughly also about the atmosphere of planet Venus.
Venus surface is so hot because of the 90times bigger mass than our atmosphere.
A planet atmosphere (also Mars, Jupiter…) is like a pullover.
How warm you feel in the winter depends how thick the pullover is – just a little bit on the colour of the pullover.
Do you remember how it was 60 years ago ?:
All kids should eat spinach … because of 10 times more iron in this vegetable.
Decades later it showed up that a secretary has misprinted a komma – nobody has checked it – and the whole world believed it.
I could be wrong, because I am just one man with a piece if paper and a pencil.
It is not correct to say – they all lie.
You have to prove it. With numbers.
I have: max. +1,6 K global warming because of CO2 if we burn all fossile C in the next centuries.
Am I wrong ?:
Control this:
https://www.schottie.de/?p=87
https://www.schottie.de/?p=11809
Danke lieber Gerhard,
Ich erkenne eine Grafik und sehe daher, woher sie kommt. Sie können das nicht glauben, aber alle Probleme mit dem Klimawandel sind völlig falsch.
Ich weiß nicht, ob ich dir das schon gesagt habe, aber mein Professor für Chemie an der Universität Brüssel ist ein alter Mann, aber sehr klug (er macht viel Sport). Sie erklären mir die gesamte Physik der Atmosphäre mit vielen physikalischen Gleichungen. Und es ist klar, dass es keinen Treibhauseffekt des CO2 gibt. Die Basis von allem ist einfach falsch. Ich werde Ihnen separate Links des von ES veröffentlichten Papiers senden .
Wir zerstören unsere Wirtschaft, unsere Gesellschaft, unsere Zukunft auf der Grundlage falscher Physik.
Gesendet: Freitag, 14. Mai 2021 um 00:17 Uhr
Von: "Gerhard Sabathil"
An: "Schottlaender Rainer"
Betreff: Fwd: Zur Erwärmung der Erdatmosphäre durch CO2 – Schottie.de
Von meinem iPhone gesendet
Anfang der weitergeleiteten Nachricht:
Von: Samuel Furfari
Datum: 13. Mai 2021 um 13:52:06 MESZ
An: Gerhard Sabathil
Betreff: Aw: Zur Erwärmung der Erdatmosphäre durch CO2 – Schottie.de
Thanks dear Gerhard,
I recognise some graph and therefore I see where is coming from.you cannot believe that but All climate change issue is totally fake.
I don't know if I told you that already but my professor of chemistry at Brussel University is an old man but very bright (he is making a lot of sport ). You explain me all the physics of the atmosphere with a lot of physics equations.and it is clear that there is no greenhouse effect of the CO2.the base of everything is just wrong.I will send you separately links of the paper that ES published.
We are destroying our economy, our society, our future on the basis of wrong physics.
Samuel Furfari
Les problèmes d'aujourd'hui doivent être traités avec les solutions d'aujourd'hui qui ont été conçues par les ingénieurs ; les problèmes de demain seront résolus avec les solutions de demain qui seront également conçues par les ingénieurs., a écrit :
Le 13 mai 2021 à 11:20 +0200, Gerhard Sabathil
Can you translate and understand dear Sam?
He proves against climate change
Regards G
https://www.schottie.de/?p=11809
Von meinem iPhone gesendet
Nachtrag. update :
Gesendet: Sonntag, 16. Mai 2021 um 08:42 Uhr, gsabathil@icloud.com
Von: "Rainer Schottlaender"
An: "Samuel Furfari"
Cc: "Martin …
Betreff: Good morning Samuel …
Aw: There is no correlation between global temperature and CO₂ concentration in the atmosphere
I have just finished a one hour musician EMail to Gerhard and have a few minutes for you
before I meet Uwe at 9 a.m. in our forest stadium for jogging:
https://de.wikipedia.org/wiki/Meeresspiegelanstieg_seit_1850 :
Der gemessene Anstieg des mittleren Meeresspiegels zwischen 1870 und 2009 beträgt ca. 25 cm
You might be are a little bit wrong, Samuel.
My rough estimation ( see thesis no. 7 of 37 here: https://www.schottie.de/?p=46 )
is that maybe 5 of these 25 cm are human made.
The rest, 20 cm seems to be post-glacial.
I think – like in a thermometer – the ocean level is the best measure for a "global temperature"
How you measure "Global TLT" ?
It is clear that there has to be a small CO2 influence on T.
For sure because Cp (CO2) differs a little bit from Cp(O2,N2)… but this is a very small effect.
It is not so easy to decide as you think in this minute, Samuel.
8-44 a.m ready for takeoff
Gesendet: Sonntag, 16. Mai 2021 um 08:16 Uhr, "Rainer Schottlaender"
Von: "Samuel Furfari"
An: "Gerhard Sabathil"
Cc: "Martin…
Betreff: There is no correlation between global temperature and CO₂ concentration in the atmosphere
This graph says it all…you don't have to be a scientist to observe that there is no correlation between the 55 ppm per year increase in CO₂ concentration and the fluctuating global temperature measured by satellite around a stable average.
Samuel Furfari
https://de.wikipedia.org/wiki/Spezifische_W%C3%A4rmekapazit%C3%A4t :
Luft (trocken) 1,01
Kohlendioxid 0,846
c in kJ/(kg·K) = J/gK
Was sehe ich wenn ich aus dem Fenster schaue ?
Einen schönen neuen Tag.
Die Klimakatastrophe findet in den Köpfen statt – nicht in der Wirklichkeit.
Ich habe nachgerechnet:
Maximal + 1,6 K globale Erwärmung durch CO2 sind physikalisch möglich.
Ich kann mich irren.
Ich bin nur ein Mann mit Papier, Bleistift und einem wachen 71jährigem Verstand.
Ich erwarte von Ihnen – heute in meiner Eigenschaft als Mehrwertsteuerbürger –
die Beantwortung meiner Frage nach dem zu erwartenden Strahlungsverlust m/eines
vorerst hypothetischen 300 Mio K / 1 mysec / D2 – Blitzkanals.
Das können Sie besser als ich … und dafür wurden Ihre MPI-Legionen jahrzehntelang bezahlt.
Kopie an ….
mfG
https://www.schottie.de/?p=11809
——————————————————-
Gesendet: Donnerstag, 20. Mai 2021 um 05:15 Uhr
Von: "Rainer Schottlaender"
An: info@wb-list.de
Cc: info@bdi.eu, m.schamun@bdi.eu, m.dach@bdi.eu
Betreff: Henry Marquering : Schotti for President … mach weiter so
Überweisen Sie unverzüglich und "unbürokratisch" (Zitat Ende)
1.500 (EinsFünfNullNull) Euro auf mein Ihnen bekanntes Konto.
Kostenpflichtige Nachhilfestunde für Herrn Peter Altmaier:
Vergleichen Sie Ihr jämmerliches Leben mit meinem.
Ich fahre täglich bei jedem Wetter Fahrrad, lebe spartanisch, fröhlich und kerngesund.
Daran könnten Sie sich mit Ihrem ungesunden Übergewicht ein Vorbild nehmen.
Ich habe mir sogar problemlos und wohltuend zur Zeit das Rauchen und das Kiffen abgewöhnt.
Ihrem Lebenslauf entnehme ich, dass Sie einer der zahllosen überbezahlten Juristen
und anderer Geschwätzwissenschaftler in Deutschland sind.
Die unser Land nicht braucht.
Ihr angeblicher Rechtsstaat ist schon lange unter die Räder zu vieler dicker Daimler gekommen.
Sie versenken seit Jahrzehnten in Ihrem Subventionsministerium Milliardenbeträge.
Ich bin 71 Jahre alt.
Als ich geboren wurde, arbeiteten 500.000 Menschen im Ruhrgebiet in der Kohleindustrie.
10 Millionen verlorene Arbeitsplätze der Stahl-Textil-Elektronik und vieler anderer Industrien
hat Ihr angeblicher Sozialstaat im Laufe der Jahrzehnte in alle Welt exportiert.
Sie kündigen lautstark schwarze Nullen und andere Finanzlügen an.
Billionenschulden und Verpflichtungen lasten auf der jungen Generation.
Für die Sie mit nichts haften.
Ich forsche seit 1990 täglich ca. 3 Stunden , also ca. 30.000 unbezahlte Arbeitsstunden,
an Fragen rund um das Thema Energie.
Was treibt mich trotzdem immer wieder an ?:
Ich habe mehrere weltweit neue ,
von Ihnen und Ihrer unfähigen Regierung ignorierte Ergebnisse erzielt.
Betrachten Sie die 1.500 Euro,
die Sie mir auch gerne heute in bar hier im schönen Jastrower Weg vorbeibringen können,
als Anzahlung.
mfG
https://www.schottie.de/?page_id=56
Rainer Schottlaender
t2SScpoan0sd Soturetd.adg ·
Mit Öffentlich geteilt
Öffentlich
Gesendet: Mittwoch, 19. Mai 2021 um 08:13 Uhr
Von: "Rainer Schottlaender"
An: buergerdialog@bmwi.bund.de, Corona-Kontrolle@ibb.de, Internetpost@bundesregierung.de, Bueko_1501_Berlin@web.de, info@bdi.eu, m.schamun@bdi.eu, m.dach@bdi.eu
Lieber Herr Schottlaender -ich habe sehr, sehr herzlich lachen müssen…Sie sind großartig!!! Ich bewundere Ihre Ausführungen hinter denen ein ungeheures WISSEN steckt -mein Gott.
Ich bin 81 und fühle mich wie 25—naja -so sportlich wie damals nicht mehr aber die Gesundheit ist ok. Ich bin Bankkaufmann, Volkswirt und seit Jahrzehnten vielseitiger Unternehmer (aktuell u.a. http://www.fashion-square-shops.de), also kein Physiker, Mathematiker oder Wissenschaftler -aber sehr neugiiierig und interessiere mich für fast alles (außer Fußball und Formel 1)
Kein Wunder, dass ich auch über CO2 gestolpert bin und die Klimafrage. Seit einigen Jahren befasse ich mich damit und setze auf Menschenverstand und 2 plus 2. Ich habe schnell verstanden -simpel und laienhaft ausgedrückt – das IR Strahlen und CO2 kein Miteinander haben (absorption der Strahlen und Rücksendung zum Boden etc…) und den dummen Vergleich mit einem Treibhaus.
Bei intensiverer Recherche kam ich bald hinter den ganzen Schwindel und habe verstanden was eine Finanzmafia -unter Führung des sog. IPCC – da im Schilde führt. Mit üblen Mitteln und mit bekanntem Konzept, die Menschen zunächst in Angst und Schrecken zu versetzen (mit Hilfe gekaufter Medien), um dann eigene wirtschaftliche Pläne zu realisieren. (Weg mit Kohle, Öl und Gas etc. und eine neue Wirtschaftsordnung implementieren) CO2 ist eine simple Sache und eine Klimakatastrophe über CO2 an die Wand zu malen recht einfach (für einfache Menschen)
Ihre Ausführungen habe ich vollständig aber mit großer Geschwindigkeit gelesen -natürlich die wissenschaftlichen Dinge nicht -davon habe ich NULL Ahnung, kann aber einiges verstehen und in vielen Aussagen konnte ich – für mich verständlich (im langsam DENKEN bin ich schlecht)-meine Erkenntnisse bestätigt finden. Ihre so umfangreichen Analysen etc. werden sicherlich von kaum irgendwelchen Schlaumeiern verstanden und die, die sie verstehen müssten sind schon "eingekauft". Ich habe mit einigen der bekannten Namen (die auch durch die Talkshows turnen) gemailt aber nur dumme Antworten erhalten und ein "um- den- Brei-herumgelaber".
Die gekauften Medien schirmen alles ab und unsere Kanzlerin ist mit von der Partie und ja auch persönlich bekannt mit Bill Gates. Sie findet auch THE Great Reset" vernünftig und damit den chinesischen Kommunismus "CCP". Der Sohn von Klaus Schwab (Davos) hat für seinen Vater 10 Jahre in China gearbeitet….
Sie müssten ARD,ZDF, Welt etc. und die Talkshowtypen gewinnen um da mal mit anderen eine Diskussion führen zu können…wird aber wohl schwer fallen -wenn überhaupt bei denen Interesse besteht. Vielleicht gibt es ja eine unverdorbenen, ehrlichen Journalisten der da was aufbauen könnte.
Corona kommt aus dem selben Lager, die Pandemie besteht nicht -es sind die idiotischen PCR Tests die nichts beweisen und die blöden "Inzidenzien" mit denen Basiszahlen für die Pandemie "erstellt" werden und wieder wird das Volk in Angst und Schrecken versetzt. Die EXDDR "Mutti" wurde ja auf die Kanzlerposition geschoben: Kohl -der unerkannt blieb aber auch dazu gehörte :"mein Mädchen" und "Mutti" leistete gute Arbeit -hahaha, zerstörte Deutschland und Europa und bereitete den crash vor…aber das ist ein anderes Thema.
Das RKI Institut -eine Behörde der Regierung -(!) mit Dr. Wielens an der Spitze – und dem wundersamen "Dr." (?) Drosten – beide arbeiten im Interesse der WHO -und damit kommen wir zu einer wesentlichen Figur: der Finanzmafia und ein Flagschiff: Bill Gates. (Dem scheint es jetzt an den Kragen zu gehen: bei Microsoft musste er seinen Vorstandssitz räumen (sex.Probleme schlimmster Art -so wird berichtet)
Zusammenfassend: Ich bin sehr erfreut, dass Sie die selben Erkenntnisse -wissenschaftlich toll begründet -haben wie ich, das freut einen Laien.
Die allerbesten Grüße aus Düsseldorf.
Ihr Hans-H.Wiethoff
"Wissenschaftlich toll begründet". Stimmt. Ich habe in Leipzig Mathematik studiert. Ich fand es gut, das zu tun. Aber es interessierte niemanden in meinem Umfeld. Meine Mutter meinte später, als ich heiratete: "Junge, Du musst lernen, ein Haushaltbuch zu führen." Mathe hatte wohl mit dem Leben wenig zu tun. Nach Mathe begann ich Theologie zu studieren. Dort wollten Sie mir Glauben herleiten, beweisen, erklären. Als ich sagte: "Glauben habe ich schon!", passte das wieder nicht zu den Ausbildungszielen. Ich hatte noch viele solche Lebensabschnitte und Erfahrungen. Nun bin ich fast 70, und sie meinen seit einiger Zeit, dass es gut für mich wäre, mich der allgemeinen Angstpsychose anzuschließen.
Kann mir mal einer sagen, wozu das gut sein soll.
Ich kann zwar den wissenschaftlichen Beweisketten nicht mehr folgen, aber sie haben mein Vertrauen.
Die Angstmacher, Politiker, Lobbyisten und Medien lügen sich – nicht nur zum Klima -eine falsche Welt zusammen. Dafür gibt es sehr schlüssige Beweise, die nicht an einer Vorbildung hängen: Ganz einfach gesagt – es gibt heute dank der Smartphones wirklich Millionen Video-Aufnahmen, die Polizei- und Staatsgewalt gegen friedliche, unbewaffnete demonstrierende Menschen zeigen und beweisen. Das sind echte, wissenschaftliche Beweise, und diese Beweise könnte jeder leicht verstehen.
Aber sie kommen einfach weg, werden verschwiegen und gelöscht.
Und auch diese Klima-Diskussion wäre längst gelöscht, wenn man befürchten müsste, dass den Erklärungen mehr als eine Handvoll Interessierter folgen würde.
Schade, das Volk der Dichter und Denker mag nicht mehr denken! Dann können wir also auch bei dem Spinat-Eisen-Kommafehler bleiben.
A propos Kommafehler: Ich bin zu DDR-Zeiten mal Aktivist mit einem Neuerervorschlag geworden, weil meine Nutzensbetrachtung mit der Formel " 10 mal 80 ist 8000" begann. Als es dann "seinen sozialistischen Gang " ging, durfte ich den Fehler nicht mehr korrigieren, weil bereits einige weitere Beteiligte auf Prämien hofften.
Gesendet: Montag, 18. Oktober 2021 um 19:02 Uhr
Von: "Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de, info@bdi.eu, m.schamun@bdi.eu, m.dach@bdi.eu, Internetpost@bundesregierung.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de, Dialog@bge.de, Planet-Wissen@wdr.de, info@bundestag.de, mail@bundestag.de, bmbf@bmbf.bund.de, info@dpa.com, mario@rtl.de, info@bild.de, Sibylle.Guenter@ipp.mpg.de, Per.Helander@ipp.mpg.de, ursel.fantz@ipp.mpg.de, Thomas.Klinger@ipp.mpg.de, Frank.Jenko@ipp.mpg.de, Eric.Sonnendruecker@ipp.mpg.de, Ulrich.Stroth@ipp.mpg.de, Robert.Wolf@ipp.mpg.de, posteingang@bmbf.bund.de, beratung@foerderinfo.bund.de, Karl.Tischler@euro-fusion.org, Volker.Naulin@euro-fusion.org, fernsehen@br.de, hartmut.zohm@ipp.mpg.de, Z27@bmbf.bund.de, hae@mpe.mpg.de, presse@unesco.de, berlin@dpa.com, ExpertenbeiratInfluenza@rki.de, wielerL@rki.de, GlasmacherS@rki.de, SchaadeL@rki.de
Betreff: Wissenschaft oder Panikmache ?
Der Treibhauseffekt:
Sendung Hoimar von Ditfurths aus dem Jahre 1978
https://www.youtube.com/watch?v=lORAR1nvfjs
heute wiederholt
geschätzt eine Million Zuschauer
Ich denke nach:
Wenn laut diesem Experiment 1.000.000 ppm CO2
37,1 – 25,8 = 11,3 Grad Erwärmung verursachen
dann würde die Anwendung des Dreisatzes ergeben,
dass weitere 100 ppm die Erde um ein Tausendstel Grad erwärmen.
Zum Treibhauseffekt
korrigiere ich die herrschende Lehrmeinung:
https://www.schottie.de/?p=87
Zur Erwärmung der Erdatmosphäre durch CO2
Glaubt man den täglichen Nachrichten, dann bedroht
eine globale Erwärmung die Menschheit.
Dafür sei das Treibhausgas CO2 hauptverantwortlich.
Klimaskeptiker bezweifeln, dass der Temperatur-Anstieg menschengemacht ist.
Was passiert,
wenn wir auf der Erde in den nächsten Jahrhunderten
fossilen Kohlenstoff nutzen wie bisher ?
In Zahlen:
Ich untersuche das dann im Jahr 2300 mögliche Scenario von 1600 ppm statt heutiger 400 ppm :
Zur Erwärmung der Erdatmosphäre durch CO2
von Rainer Schottlaender, Diplomphysiker
dT/dH = – g/Cp beschreibt den Temperaturverlauf in einer Planetenatmosphäre
Um zu verstehen wie CO2 die Temperatur beeinflusst beginnen wir bei Null:
Bild 1 zeigt …
https://www.schottie.de/?p=11809
Gesendet: Montag, 06. September 2021 um 13:24 Uhr
Von: "Rainer Schottlaender"
An: berlin@dpa.com, Internetpost@bundesregierung.de, bmbf@bmbf.bund.de, Z27@bmbf.bund.de, Dialog@bge.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, mail@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de, info@bundestag.de, bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de
Betreff: Inflation oder Hyperinflation ?
100 €/$ Billionen Weltschuldensumme im Jahr 2008
300 €/$ Billionen heute
= 4 Welt-Bruttoinlandsprodukte
Milliardenverschwender und Billionenbetrüger Staat
https://www.schottie.de/?p=10372
DAX 1959–2015 ………..
400 ……………….. 16.000 heute
Gesendet: Donnerstag, 09. September 2021 um 12:47 Uhr
Von: "Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de, info@bdi.eu, m.schamun@bdi.eu, m.dach@bdi.eu, Internetpost@bundesregierung.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de, Dialog@bge.de, Planet-Wissen@wdr.de, info@bundestag.de, mail@bundestag.de, bmbf@bmbf.bund.de, info@dpa.com, mario@rtl.de, info@bild.de, Sibylle.Guenter@ipp.mpg.de, Per.Helander@ipp.mpg.de, ursel.fantz@ipp.mpg.de, Thomas.Klinger@ipp.mpg.de, Frank.Jenko@ipp.mpg.de, Eric.Sonnendruecker@ipp.mpg.de, Ulrich.Stroth@ipp.mpg.de, Robert.Wolf@ipp.mpg.de, posteingang@bmbf.bund.de, beratung@foerderinfo.bund.de, Karl.Tischler@euro-fusion.org, Volker.Naulin@euro-fusion.org, fernsehen@br.de, hartmut.zohm@ipp.mpg.de, Z27@bmbf.bund.de, hae@mpe.mpg.de, info@dpa.com
Betreff: B"M"BF … IPP … ergänzend zur Entlassung der unfähigen Forschungsministerin Anja Karliczek
Wieviel Prozent der Energie eines normalen Gewitterblitzes landen
– im Blitzkanal ( … und entladen sich dann als Donner ..) ?
– im Einschlagpunkt ?
Ich prüfe meine dem IPP und dem B"M"BF vorliegende bisher ungeprüfte Idee,
Kernfusion durch die Blitzentladung
einer zB 400 MJ Kondensatorbank
bei Normaldruck
von 170 kg D2 Gas in einem 1000 m^3 Behälter
durch den Pincheffekt zu zünden.
Mit freundlichen Grüssen
https://www.schottie.de/?page_id=56
an
https://en.wikipedia.org/wiki/Marcos_Rubinstein
https://en.wikipedia.org/wiki/Farhad_Rachidi
https://www.iclp-centre.org/index.php
Gesendet: Donnerstag, 09. September 2021 um 12:11 Uhr
Von: "Rainer Schottlaender"
An: schuster@tuhh.de
Betreff: Frage an Prof. Schuster, Rachidi, Rubinstein
Gesendet: Mittwoch, 08. September 2021 um 11:30 Uhr
Von: "Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de, info@bdi.eu, m.schamun@bdi.eu, m.dach@bdi.eu, Internetpost@bundesregierung.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de, Dialog@bge.de, Planet-Wissen@wdr.de, info@bundestag.de, mail@bundestag.de, bmbf@bmbf.bund.de, info@dpa.com, mario@rtl.de, info@bild.de, Sibylle.Guenter@ipp.mpg.de, Per.Helander@ipp.mpg.de, ursel.fantz@ipp.mpg.de, Thomas.Klinger@ipp.mpg.de, Frank.Jenko@ipp.mpg.de, Eric.Sonnendruecker@ipp.mpg.de, Ulrich.Stroth@ipp.mpg.de, Robert.Wolf@ipp.mpg.de, posteingang@bmbf.bund.de, beratung@foerderinfo.bund.de, Karl.Tischler@euro-fusion.org, Volker.Naulin@euro-fusion.org, fernsehen@br.de, hartmut.zohm@ipp.mpg.de, Z27@bmbf.bund.de, hae@mpe.mpg.de, info@dpa.com
Betreff: ergänzend … zur Entlassung der unfähigen Forschungsministerin Anja Karliczek
Für den Schutz der Erde vor einem Treffer durch einen erdbahnkreuzenden Asteroiden oder Kometen,
auch NEO = Near Earth Object genannt,
ist notwendig:
1. Die Änderung des Atomwaffensperrvertrages durch die UNO.
Das Manöver und der Nuklearschlag müssen berechnet und geübt werden.
Dafür sind regelmässige Tests – zB auf dem Mond – notwendig.
2. Aufrüstung der bisher je ca. 500 Stück ICBMs der USA und Russlands.
Dafür sind erforderlich und genügen
je einige sofort startklare geboosterte ICBMs,
die 16 km/s statt bisher 7 km/s erreichen.
Literatur:
Mein Proposal A 267 SBIR/DOD vom 5. Juli 1990
https://www.schottie.de/?p=9755
https://www.schottie.de/?p=11545
Gesendet: Samstag, 26. Dezember 2020 um 09:23 Uhr
Von: „Rainer Schottlaender"
An: cneos@jpl.nasa.gov, pchodas@jpl.nasa.gov, letters@washpost.com, BerlinPCO@state.gov
Betreff: Fw: NEO defense
NASA's planned distraction – only 3 km deflection during one year from Didymos through DART –
will not work:
Earth diameter 12,740 km / 3 km = 4,250 times more impulse transmission is required:
Either 4,250 probes would have to hit Didymos.
Or 1 (one) atomic bomb.
Copyright: https://www.schottie.de/?p=11545#comment-130784
Best regards
Rainer Schottlaender,Dipl.-Phys.
D- 12587 Berlin
https://www.schottie.de/?p=9755
an
https://www.unesco.de/ueber-uns/ueber-die-duk/kontakt
Gesendet: Mittwoch, 08. September 2021 um 10:20 Uhr
Von: "Rainer Schottlaender"
An: presse@unesco.de
Betreff: UNESCO … Prof. Dr. Maria Böhmer (Präsidentin), Prof. Dr. Christoph Wulf (1. Vizepräsident), Prof. Dr. Hartwig Carsten Lüdtke (2. Vizepräsident), Dr. Roman Luckscheiter (Generalsekretär), Dr. Lutz Möller
Gesendet: Dienstag, 07. September 2021 um 09:31 Uhr
Von: "Rainer Schottlaender"
An: Sie
Betreff: Entlassung der unfähigen Forschungsministerin Anja Karliczek
Wenn auch aus anderem Grund stimme ich der „atomaren Rolle rückwärts" von Frau Merkel im Jahr 2011 zu:
Die weitere Nutzung des extrem seltenen Isotops U-235 ( 7 kg pro Tonne Natururan )
in allen deutschen und fast allen AKWs weltweit ist Verschwendung der Welt-Uran-Reserven.
2. Erforderlich ist die Klärung die Frage des ob und wie
einer zukünftigen Plutoniumwirtschaft oder Thoriumwirtschaft.
Am Schnellen Brüter ( U238 ==>Pu239) arbeiten weltweit viele Teams.
Den von mir vorgeschlagenen U-233 Produktionsreaktor gibt es weltweit bisher nicht.
3. Erforderlich ist weiterhin die Klärung des Endlagerproblems.
Mein Vorschlag hierzu: https://www.schottie.de/?p=11405
4. Die Frage, wie CO2 die bodennahe Lufttemperatur beeinflusst ist ungeklärt.
Nach meinen Berechnungen besteht keine Gefahr : https://www.schottie.de/?p=11809
Literatur hierzu:
https://www.schottie.de/?p=11424#comment-136331
mfG
https://www.schottie.de/?page_id=56
4. Erwarte und fordere ich als Physiker und Mehrwertsteuerbürger von DEMO-Reaktor-Chef Zohm und dem IPP
nach 73 erfolglosen Tokamakjahren die Beantwortung meiner Fragen
zu meiner Ihnen vorliegenden grob skizzierten Idee,
wie man einen D2 Kernfusionsreaktor besser und schneller als ITER bauen könnte.
mfG
https://www.schottie.de/?page_id=56
Gesendet: Sonntag, 05. September 2021 um 13:29 Uhr
Von: "Rainer Schottlaender"
An: berlin@dpa.com
Betreff: Klimaismus – eine neue Weltreligion
"Wissenschaftler",
die keine zehn Tage das Wetter vorhersagen können,
behaupten zu wissen was passiert,
wenn die Menschheit weiter wie bisher fossilen Kohlenstoff nutzt.
Ich habe versucht das zu berechnen :
Zur Erwärmung der Erdatmosphäre durch CO2
https://www.schottie.de/?p=11809
————————————————————————————————-
INFLATION – MASSENARBEITSLOSIGKEIT – ALTERSARMUT – EINE BETROGENE JUNGE GENERATION.
Genau das wird
beschleunigt durch das absurde, destruktive und zerstörerische Ziel
einer „Dekarbonisierung ohne Kernenergie" (Merkel)
hierzulande passieren und eskalieren.
https://www.schottie.de/?p=11424#comment-138097
Gesendet: Dienstag, 10. August 2021 um 14:01 Uhr
Von: "Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de, Internetpost@bundesregierung.de, bmbf@bmbf.bund.de, Z27@bmbf.bund.de, Dialog@bge.de, buergerdialog@bmwi.bund.de…
Betreff: Unfähigkeit der Regierung Merkel
Wenn Sie, der Leser dieser EMail, ich oder irgendein Bürger dieses Landes,
sich heute oder in Zukunft mit Corona oder einem anderen pandemischen Virus infizieren,
dann ist der richtige Ort für eine Behandlung
nicht ein für den Normalbetrieb ausgestattetes Krankenhaus
sondern ein Lazarett.
Die Unfähigkeit des deutschen Staates – nicht nur in dieser Sache – beweist diese
Risikoanalyse im Bevölkerungsschutz 2012
https://dserver.bundestag.de/btd/17/120/1712051.pdf
Ich zitiere Seite 64:
Für den gesamten zugrunde gelegten Zeitraum von drei Jahren ist in Deutschland mit mindestens
7,5 Millionen Toten
als direkte Folge der Infektion zu rechnen…"
9 Jahre lang hat nicht einer der "Verantwortlichen"
in diesem an Haupt und Gliedern verfaultem Staat
auf diese Warnung reagiert.
—————————————-
Sofort an den hierfür zuständigen Bundespräsidenten
Gesendet: Dienstag, 25. Mai 2021 um 14:16 Uhr
Von: „Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de
Cc: Internetpost@bundesregierung.de, bmbf@bmbf.bund.de, Z27@bmbf.bund.de, Dialog@bge.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, mail@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de, info@bundestag.de
Betreff: Entlassung der unfähigen Ministerin Anja Karliczek
Wegen durch den BMBF verursachter Schäden am Vermögen der Bundesrepublik Deutschland
in mehrstelliger Milliardenhöhe.
Aufgrund mangelhafter wissenschaftlicher Grundlage, Qualifikation,
verfehlter Bewertungen und Förderungen.
Zahlreiche vergangene, laufende und geplante Ausgaben betreffend.
Durch Frau Karliczek und viele in diesem Organigramm
namentlich erwähnten Personen und „Forschungs"projekte:
https://www.bmbf.de/upload_filestore/pub/orgplan_eng.pdf
Wegen Ignorierung meiner zukunftsweisenden Projekte
EARTH-1, U-233 Produktionsreaktor, CO2 und D2 Fusion.
Mit freundlichen Grüssen
Rainer Schottlaender, Dipl.-Phys,
12587 Berlin
https://www.schottie.de/?page_id=56
Literatur:
Ich kündige den Weltklimavertrag
Kohlenstoff und Kernenergie sind das Fundament unserer Volkswirtschaft
https://www.schottie.de/?p=11424
GROSSER MUND UND KLEINE OHREN – DEUTSCHLANDS KLIMA-PROFESSOREN
https://www.schottie.de/?p=5449
37 Thesen für CO2 :
1. Kohlendioxyd ist ein lebensspendendes Nutzgas, ohne das keine Pflanze wächst
und dem alle Industriestaaten den in Jahrhunderten erworbenen Reichtum verdanken
https://www.schottie.de/?p=46
Zur Erwärmung der Erdatmosphäre durch CO2 :
https://www.schottie.de/?p=11809
EARTH-1 :
Die neue, weltweit kaum erforschte Idee einer Endlagerung von Atommüll tief im Erdmagma
ist vermutlich millionenjahresicher und technisch machbar :
https://www.schottie.de/?p=11405
Ich warne VW, Daimler und BMW :
https://www.schottie.de/?p=11654
Das WOOD-SCHOTTLAENDER-EXPERIMENT
https://www.schottie.de/?p=87
image.png
Historisches Beispiel für einen jahrzehntelangen weltweiten Irrglauben:
https://de.wikipedia.org/wiki/Gustav_von_Bunge
… war der Urheber der Annahme,
Spinat wäre durch einen besonders hohen Eisengehalt dem Muskelaufbau förderlich.
Allerdings bezog sich der von Bunge 1890 bestimmte Wert von 35 mg Eisen auf 100 g Spinatpulver
und lag damit 10-mal höher als der Eisengehalt von frischem Spinat…"
https://youtu.be/OwqIy8Ikv-c
I have listened these 5 minutes and agree with every single word of Prof. Richard Lindzen.
Most of this I have already known and published in the 1990`s : https://www.schottie.de/?p=46
Before we look deeper into the physics let me try a social experiment:
I imagine my audience is Greta Thunberg and 50.000 of her fanatic fans in the London Wembley Stadium.
How would I argue ?
If I get the microphone for one minute:
Each of you her is asking the right question.
If the earth becomes uninhabitable because of CO2 then we have to act immediately.
Even faster and more drastic than you ask.
But consider the consequences before you act.
For your own life.
What if you are wrong?
If I'm wrong … I'll give back my physics diploma.
Do you do the same with your doctorate, Mrs. Merkel?
The consequences of a world without the use of fossil carbon and nuclear energy
are so drastically
that the CO2 question needs to be answered without any doubt.
Meine Kontonummer DE92 1005 0000 1674 8053 45 BELADEBEXXX
Das Weiterleiten dieser EMail ist erkenntnisfördernd und produktiv
Mit Benennung meines Copyrights https://www.schottie.de
———————————————————————————————————
Kostenpflichtige Nachhilfestunde für Herrn Peter Altmaier:
Vergleichen Sie Ihr jämmerliches Leben mit meinem.
Ich fahre täglich bei jedem Wetter Fahrrad, lebe spartanisch, fröhlich und kerngesund.
Daran könnten Sie sich mit Ihrem ungesunden Übergewicht ein Vorbild nehmen.
Ich habe mir sogar problemlos und wohltuend zur Zeit das Rauchen und das Kiffen abgewöhnt.
Ihrem Lebenslauf entnehme ich, dass Sie einer der zahllosen überbezahlten Juristen
und anderer Geschwätzwissenschaftler in Deutschland sind.
Die unser Land nicht braucht.
Ihr angeblicher Rechtsstaat ist schon lange unter die Räder zu vieler dicker Daimler gekommen.
Sie versenken seit Jahrzehnten in Ihrem Subventionsministerium Milliardenbeträge.
Ich bin 71 Jahre alt.
Als ich geboren wurde, arbeiteten 500.000 Menschen im Ruhrgebiet in der Kohleindustrie.
10 Millionen wertschöpfende Arbeitsplätze der Stahl-Textil-Elektronik und vieler anderer Industrien
hat Ihr angeblicher Sozialstaat im Laufe der Jahrzehnte in alle Welt exportiert.
Sie kündigen lautstark schwarze Nullen und andere Finanzlügen an.
Billionenschulden und Verpflichtungen lasten auf der jungen Generation.
Für die Sie mit nichts haften.
Ich forsche seit 1990 täglich ca. 3 Stunden , also ca. 30.000 unbezahlte Arbeitsstunden,
an Fragen rund um das Thema Energie.
Was treibt mich trotzdem immer wieder an ?:
Ich habe mehrere weltweit neue ,
von Ihnen und Ihrer unfähigen Regierung ignorierte Ergebnisse erzielt.
Betrachten Sie die 1.500 Euro, die Sie mir auch gerne heute in bar
hier im schönen Jastrower Weg vorbeibringen können, als Anzahlung.
mfG
https://www.schottie.de/?page_id=56
—————————————————————————————————
ICH BIN DAS VOLK … in dieser Sache :
In Deutschland koste ein Personalausweis,
Führerschein und Reisepass ab heute 10 Euro.
Dieser bürgerfreundliche neue Gesetzesvorschlag ersetzt drei Seiten Gebührentabellen
und erspart jedem Bürger einige hundert Euro pro Leben.
Ich habe im Amt für Bürger"dienste" Berlin-Köpenick meinen Widerspruch
gegen die bisher nach Gutsherrenart erzwungenen überhöhten Gebühren eingereicht.
Zehn Euro sind kostendeckend für Produktion und Verwaltung.
—————————————————————————————————–
Gesendet: Mittwoch, 26. Mai 2021 um 13:35 Uhr
Von: „Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de
Cc: ExpertenbeiratInfluenza@rki.de, wielerL@rki.de, GlasmacherS@rki.de, SchaadeL@rki.de, Internetpost@bundesregierung.de, bmbf@bmbf.bund.de, Z27@bmbf.bund.de, Dialog@bge.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, mail@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de, info@bundestag.de, mario@rtl.de
Betreff: Leistungsvergleich und Unfähigkeitsnachweis für Peter Altmaier … zZt. B"M"Wi
130 Milliarden Stück Einweg-Mundschutz weltweit
– ntv heute am 26. Mai 2021 um 12 Uhr 50 –
belasten inzwischen die Umwelt und die Haushalte.
Gesendet: Samstag, 25. April 2020 um 07:02 Uhr :
In meine Hausapotheke kommt für dieses Jahr und als Pandemievorsorge ein Päckchen
wiederverwendbarer Mundschutz aus geeignetem waschfestem Material.
Für unter 20 Euro.
Copyright: www.schottie.de
Ärztinnen und Ärzte am RKI und in Deutschland:
MENS SANA IN CORPORE SANO !
Sieht so ein gesunder Körper aus,
dessem gesunden Geist und Rat ich folgen sollte ?:
Peter Altmaier auf dem 29. Parteitag der CDU Deutschlands am 6. Dezember 2016 in Essen
—————————————————————————————————————————————
zur Verschwendung von mehr als einer Milliarde Euro öffentlicher Gelder ……. Tag 33 nach der Kontaktsperre am 23. März
Beweismittel für das Verfahren VG 23 K 152/20 am Verwaltungsgericht Berlin
Ärztinnen und Ärzte am Robert-Koch-Institut:
Überlebt das Coronavirus einen Vollwaschgang bei 90 Grad in meiner Waschmaschine ?
„BUNDESREGIERUNG RECHNET MIT EINEM BEDARF VON ZWÖLF MILLIARDEN SCHUTZMASKEN"
… brüllte das Staatsfernsehen.
Ich denke nach:
Dividiert durch 80 Millionen deutsche Staatsbürger älter als 3 Jahre … ergibt 150 Stück pro Jahr.
Meine Apothekerin verlangte 2 Euro pro Mundschutz … ergibt
300 Euro pro Jahr … pro Familienmitglied.
Von meinem Rest-Netto.
Gesendet: Samstag, 25. April 2020 um 07:02 Uhr
Von: „Rainer Schottlaender"
An: ExpertenbeiratInfluenza@rki.de, wielerL@rki.de, GlasmacherS@rki.de, SchaadeL@rki.de…
Cc: mario@rtl.de …
https://www.schottie.de/?p=11424#comment-136331
—————————————————————————————-
Merkels „Fach"kräfte :
Scholz – Jurist
Maas – Jurist
Altmaier – Jurist
Seehofer – Diplom-Verwaltungswirt
Lambrecht – Jurist*in
Heil – Politik"wissenschaft"ler
AKK – Jurist*in
Klöckner – Politik"wissenschaft"lerin
Giffey – „Rechts"pflegerin
Spahn – Bankster + Jurist + Quotenschwuler
Scheuer – Politik"wissenschaftler"
Schulze – Politik"wissenschaft"lerin
Karliczek – Bankkauffrau … bei der Deutschen Bank
Müller – Studium der Pädagogik, Politik- und Wirtschafts"wissenschaft"en
Braun – Studium der Humanmedizin ( Fachkraft für Narkose)
https://www.bundesregierung.de/breg-de/bundesregierung/bundeskabinett
https://www.schottie.de
—————————————————————————————
Gesendet: Montag, 31. Mai 2021 um 21:23 Uhr
Von: „Rainer Schottlaender"
An: „Samuel Furfari" , gsabathil@icloud.com
Betreff: Aw: Wegen Zustimmung zum Atomausstieg: Vorwürfe gegen Ethikkommission – WELT
1. Wenn auch aus anderem Grund stimme ich der „atomaren Rolle rückwärts" von Frau Merkel im Jahr 2011 zu:
Die weitere Nutzung des extrem seltenen Isotops U-235 ( 7 kg pro Tonne Natururan )
in allen deutschen und fast allen AKWs weltweit ist Verschwendung der Welt-Uran-Reserven.
2. Erforderlich ist die Klärung die Frage des ob und wie
einer zukünftigen Plutoniumwirtschaft oder Thoriumwirtschaft.
Am Schnellen Brüter ( U238 ==>Pu239) arbeiten weltweit viele Teams.
Den von mir vorgeschlagenen U-233 Produktionsreaktor gibt es weltweit bisher nicht.
3. Erforderlich ist weiterhin die Klärung des Endlagerproblems.
Mein Vorschlag hierzu: https://www.schottie.de/?p=11405
4. Die Frage, wie CO2 die bodennahe Lufttemperatur beeinflusst ist ungeklärt.
Nach meinen Berechnungen besteht keine Gefahr : https://www.schottie.de/?p=11809
Literatur hierzu:
https://www.schottie.de/?p=11424#comment-136331
mfG
https://www.schottie.de/?page_id=56
————————————————————————————
Gesendet: Samstag, 05. Juni 2021 um 07:45 Uhr
Von: „Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de
Cc: info@bdi.eu, m.schamun@bdi.eu, m.dach@bdi.eu, Internetpost@bundesregierung.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de, Dialog@bge.de, Planet-Wissen@wdr.de, info@bundestag.de, mail@bundestag.de, „Z27 Posteingang" , bmbf@bmbf.bund.de
Betreff: Guten Morgen Herr Bundespräsident
Der Niedergang von Deutschlands Industrie findet in Zeitlupe statt.
Jahr für Jahr.
Billion für Billion.
Finanziert durch die Notenpresse.
Beschleunigt durch die Energiewende.
Inflation, Massenarbeitslosigkeit und Altersarmut erwarten dieses Land.
Copyright: https://www.schottie.de
Betreff:
Entlassung der unfähigen Ministerin Anja Karliczek
Gesendet an Sie am Dienstag, 25. Mai 2021 um 14:16 Uhr
Begründet und veröffentlicht hier:
https://www.schottie.de/?p=11424#comment-136331
————————————————————
Gesendet: Dienstag, 08. Juni 2021 um 07:33 Uhr
Von: „Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de, info@bdi.eu, m.schamun@bdi.eu, m.dach@bdi.eu, Internetpost@bundesregierung.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de, Dialog@bge.de, Planet-Wissen@wdr.de, info@bundestag.de, mail@bundestag.de, „Z27 Posteingang" , bmbf@bmbf.bund.de, info@dpa.com, mario@rtl.de, info@bild.de
Betreff:
„Dekarbonisierung ohne Kernenergie" … ist ein gemeingefährlicher Kindertraum
Heute im Baumarkt:
Lieferengpässe wie zu D"D"R-Zeiten.
Momentan coronabedingt …
… wird das Problem von Deutschlands Industrie und Wirtschaft allmählich spürbar.
„Wir produzieren weltweit" …
Aus Made in Germany wurde … „Made in out of Germany"
Dank einer Armee unfähiger Bürohelden, die hierzulande Staat und Wirtschaft regieren.
Der Niedergang von Deutschlands Industrie findet in Zeitlupe statt.
Jahr für Jahr.
Billion für Billion.
Finanziert durch die Notenpresse.
Beschleunigt durch die Energiewende.
Inflation, Massenarbeitslosigkeit und Altersarmut erwarten dieses Land.
Copyright: https://www.schottie.de
Betreff:
Entlassung der unfähigen Ministerin Anja Karliczek
Gesendet an Sie am Dienstag, 25. Mai 2021 um 14:16 Uhr
Begründet und veröffentlicht hier
————————————
Gesendet: Samstag, 19. Juni 2021 um 14:28 Uhr
Von: „Rainer Schottlaender"
An: Sie
Cc: info@dpa.com
Betreff: update … an das BPrA … an den B"M"BF … an den BDI … und an das IPP … insbesondere Herrn Hartmut Zohm
Zurück zur Kernfusion – eine wichtige Zukunftsaufgabe.
Die hoffentlich nicht endet wie der jahrhundertelang
von Kaisern und Königen finanzierte Traum vom Goldmachen aus Blei.
Die Arroganz, mit der mich die ca. 1000 von Steuergeldern bezahlten und hier mitadressierten IPP-Leute und die unfähigen Mit"arbeiter" im B"M"BF behandeln, juckt mich nicht nennenswert.
Selbstbewusst und selbstkritisch schaue ich – wie an jedem einzelnen Tag in den vergangenen 43 Jahren als schuldenfreier und erfolgreicher Kleinuternehmer – heute auf mein inzwischen 15,5 Kilogramm schweres neuestes Ideenbaby, das – öffentlich in meinem Vorgarten ausgestellt – von Jedermann begutachtet werden kann.
Von einer einfachen physikalischen Grundidee ausgehend –
ähnlich wie bei meinem Ihnen vorliegenden und bisher ignorierten
Entwurf für einen jahrelang zuverlässig arbeitenden D2 -Fusionsreaktor
gelang es mir
in nur wenigen Wochen
ohne einen Fördereuro,
mit wenig Geld und viel Kraft ,
Erfinderfreude
und täglich immer wieder neuen Anläufen und Versuchen
– vermutlich –
den Weltrekord für Wasserpumpen zu übertreffen.
Schafft es irgendwo auf der Welt eine Pumpe mit nur 1 (einer) Kilowattstunde Energieeinsatz
120 (einhundertundzwanzig) Kubikmeter Wasser 80 (achtzig) Zentimeter hoch zu fördern ?
Von einem Fluss auf ein Feld ? Für den Anbau von Reis ? In Deutschlands Kleingärten ?
Mein Prototyp 14.12 kann das…. zumindest manuell…
Montag baue ich eine hoffentlich noch bessere Druckmanschette ein
… und an einigen Stellen kann ich noch ein paar Prozent herausholen.
Die Motorisierung und die Serienproduktion ist bekannter Stand der Technik.
Das können und sollten andere Ingenieure machen.
Die können das besser und schneller als ich.
Ich bastele vermutlich nur noch ein paar Tage hier an Prototyp 14.13 herum.
Immer schön in Ruhe und langsam. Schritt für Schritt.
Wie bei meinen 3 km heute morgen auf dem Sportplatz.
Wie beim Berlin-Marathon, den ich vor zehn Jahren einmal barfuss durchjoggte.
Gesundheit ist das Wichtigste im Leben.
mfG
https://www.schottie.de/?page_id=56
Gesendet: Montag, 14. Juni 2021 um 15:27 Uhr
Von: „Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de, Internetpost@bundesregierung.de, bmbf@bmbf.bund.de, Z27@bmbf.bund.de, Dialog@bge.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de
Cc: hartmut.zohm@ipp.mpg.de, bmbf@bmbf.bund.de, „Z27 Posteingang" , Sibylle.Guenter@ipp.mpg.de, Per.Helander@ipp.mpg.de, ursel.fantz@ipp.mpg.de, Thomas.Klinger@ipp.mpg.de, Frank.Jenko@ipp.mpg.de, Eric.Sonnendruecker@ipp.mpg.de, Ulrich.Stroth@ipp.mpg.de, Robert.Wolf@ipp.mpg.de, Z27@bmbf.bund.de, posteingang@bmbf.bund.de, beratung@foerderinfo.bund.de, contact@eurofusion.org, Karl.Tischler@euro-fusion.org, Volker.Naulin@euro-fusion.org, fernsehen@br.de, Planet-Wissen@wdr.de, info@bdi.eu, m.schamun@bdi.eu, m.dach@bdi.eu
Betreff: an das BPrA … an den B"M"BF … an den BDI … und an das IPP … insbesondere Herrn Hartmut Zohm
1. Ich erinnere an meine
heute hier : https://www.schottie.de/?p=11424#comment-136331
im Internet zu findenden EMail
Sofort an den hierfür zuständigen Bundespräsidenten
Gesendet: Dienstag, 25. Mai 2021 um 14:16 Uhr
Von: „Rainer Schottlaender"
An: bundespraesidialamt@bpra.bund.de, internet-redaktion@bpra.bund.de, presse@bpra.bund.de
Cc: Internetpost@bundesregierung.de, bmbf@bmbf.bund.de, Z27@bmbf.bund.de, Dialog@bge.de, buergerdialog@bmwi.bund.de, buergerservice@uba.de, vorzimmer.peta@bundestag.de, mail@bundestag.de, presse@brh.bund.de, angela.merkel@bundestag.de,info@bundestag.de
Betreff: Entlassung der unfähigen Ministerin Anja Karliczek
2. Ich dokumentiere und begründe hiermit erneut meine berechtigten Zweifel
an den IPCC-dominierten und nur von sehr wenigen Menschen tatsächlich nachgeprüften Berechnungen zu CO2.
Mein Ergebnis finden Sie hier: https://www.schottie.de/?p=11809
Selbst wenn ich als einzelner Forscher – der nur mit Papier, Bleistift und hoffentlich auch mit 71 Lebensjahren
noch mit genug Verstand „bewaffnet" ist – mich in dieser zukunftsentscheidenden Frage verrechnet haben sollte,
so ist mit Sicherheit der momentan von Deutschland eingeschlagene Weg einer „Dekarbonisierung ohne Kernenergie"
eine verheerende Fehlentscheidung.
Falls Sie im Ernst glauben, dass 8 bis 10 Milliarden Menschen mit „alternativen" Energien sich ernähren, kleiden
und gut leben können, und wir 82 Millionen hier in Deutschland den in Jahrhunderten erarbeiteten Wohlstand zumindest
beibehalten werden – dann rate ich Ihnen sich auf ihren promovierten Hosenboden zu setzen und nachzurechnen
… was das kostet.
3. Zum Thema Zukunft der Atomenergie zitiere ich mich selbst:
Gesendet: Montag, 31. Mai 2021 um 21:23 Uhr
Von: „Rainer Schottlaender"
Betreff: Aw: Wegen Zustimmung zum Atomausstieg: Vorwürfe gegen Ethikkommission – WELT
1. Wenn auch aus anderem Grund stimme ich der „atomaren Rolle rückwärts" von Frau Merkel im Jahr 2011 zu:
Die weitere Nutzung des extrem seltenen Isotops U-235 ( 7 kg pro Tonne Natururan )
in allen deutschen und fast allen AKWs weltweit ist Verschwendung der Welt-Uran-Reserven.
2. Erforderlich ist die Klärung die Frage des ob und wie
einer zukünftigen Plutoniumwirtschaft oder Thoriumwirtschaft.
Am Schnellen Brüter ( U238 ==>Pu239) arbeiten weltweit viele Teams.
Den von mir vorgeschlagenen U-233 Produktionsreaktor gibt es weltweit bisher nicht.
3. Erforderlich ist weiterhin die Klärung des Endlagerproblems.
Mein Vorschlag hierzu: https://www.schottie.de/?p=11405
4. Die Frage, wie CO2 die bodennahe Lufttemperatur beeinflusst ist ungeklärt.
Nach meinen Berechnungen besteht keine Gefahr : https://www.schottie.de/?p=11809
Literatur hierzu:
https://www.schottie.de/?p=11424#comment-136331
mfG
https://www.schottie.de/?page_id=56
4. Erwarte und fordere ich als Physiker und Mehrwertsteuerbürger von DEMO-Reaktor-Chef Zohm und dem IPP
nach 73 erfolglosen Tokamakjahren die Beantwortung meiner Fragen
zu meiner Ihnen vorliegenden grob skizzierten Idee,
wie man einen D2 Kernfusionsreaktor besser und schneller als ITER bauen könnte.
mfG
https://www.schottie.de/?page_id=56
Gesendet: Sonntag, 20. Juni 2021 um 09:08 Uhr
Von: „Rainer Schottlaender"
An: mail@erik-marquardt.de
Cc: „Gerhard Sabathil" , „Samuel Furfari"
Betreff: Damit auch Greta Thunberg es versteht …
… erkläre ich Dir
hier und ihr wie der Treibhauseffekt tatsächlich funktioniert:
Planet Venus ist ein schönes Beispiel:
Satellitenmessungen haben bewiesen, dass es dort am Boden 464 Grad Celsius heiss ist.
Stelle Dir vor, liebe Greta, heute an diesem Hochsommertag mit 33 Grad, hättest Du
einen 1 Meter dicken Wollpullover an.
Egal welche Farbe der hat – Du würdest bald wegen Hitzschlag ins Krankenhaus kommen.
Jetzt überfordere ich Deine Schulschwänzerbildung
und wende mich an das IPCC, Deutschlands Naturwissenschaftler, Bundeskanzlerin
Doktor wofür auch immer, Angela Merkel,
die mir als Physikerin eigentlich folgen können müsste:
dT/dH = – g/Cp bestimmt den Temperaturverlauf in jeder Planetenatmosphäre.
Bei Jupiter, auf dem Mars, Venus und Erde.
Der Einfluss der Spurengase ist minimal.
Ich habe diesen abgeschätzt:
https://www.schottie.de/?p=11809
Zur Erwärmung der Erdatmosphäre durch CO2
Interessiert zwar niemanden, denn das grosse Wort führen ….
GROSSER MUND UND KLEINE OHREN –
DEUTSCHLANDS KLIMA-PROFESSOREN
Mindestens einer, nämlich ich, hat zum Glück den Überblick:
Ich kündige den Weltklimavertrag
Kohlenstoff und Kernenergie sind das Fundament unserer Volkswirtschaft.
„8. Es ist eine gefährliche Illusion zu glauben, dass wir in Deutschland unseren heutigen Lebensstandard mit einem jährlichen Energiebedarf von 500 Millionen Tonnen Steinkohle(-einheiten) = 4000 Terawattstunden (thermisch) durch „regenerative" Energien decken
… Weiterlesen … auf https://www.schottie.de … lohnt sich, nicht nur hierzu
https://de.wikipedia.org/wiki/Venus_(Planet)#Atmosph%C3%A4re :
Der starke Treibhauseffekt (man spricht hier auch vom Venus-Syndrom) ist hauptsächlich durch die Masse an Kohlendioxid bedingt, aber auch die geringen Spuren von Wasserdampf und Schwefeldioxid haben daran einen wesentlichen Anteil. Er sorgt am Boden für eine mittlere Temperatur von 464 °C (737 K).[1] Das liegt sehr weit über der ohne Treibhauseffekt berechneten Gleichgewichtstemperatur von −41 °C (232 K),[17] auch weit über den Schmelztemperaturen von Zinn (232 °C) und Blei (327 °C) und übertrifft sogar die Höchsttemperatur auf dem Merkur (427 °C).
Alles richtig, Wikipedia, nur kannst Du die zwei irreführenden Worte „an Kohlendioxyd" weglassen.
Das passiert mit jedem anderen Gas fast genauso.
Prüfe die Formel: Auf Cp kommt es an…
——————————————————————————-
Gesendet: Dienstag, 22. Juni 2021 um 09:16 Uhr
Von: „Rainer Schottlaender"
An: „Hartmut Zohm"
Cc: hae@mpe.mpg.de
Betreff: Guten Tag Hartmut Zohm
Grüssen Sie Herrn Haerendel, falls er noch lebt und fit ist.
Eine von vielen entscheidenden Fragen
zu meinem D2 Kernfusionsreaktor Entwurf:
Was passiert, wenn sich die 400 Megajoules (= 110 KWh-el = 110 Autobatterien)
der NIF Kondensatorbank
innerhalb von vermutlich Mikrosekundenbruchteilen
entladen ?
Bildet sich ein Blitzkanal in dem zB 1 Million bar Druck und 300 Mio K
hinreichend lange (Lawson-Kriterium) herrschen ?
Copyright: https://www.schottie.de
Ich veröffentliche diese EMail
an dieser besonders gelungenen und geeigneten Stelle meines blogs:
https://www.schottie.de/?p=11424#comment-136331
Seit Start des Blogs am 14.01.2011 sind 1.194.487 Besucher hier gewesen :
http://www.schottie.de